

Can we observe quantum-mechanical effects in large systems?
There are two factors that can combine to lead to observable quantum-mechanical effects in large systems.
Indistinguishable particles
Elementary particles of the same kind are identical, they cannot be distinguished from one another. Assume you put two electrons into a box. Later you let one of the electrons escape. You can never know which electron escaped and which electron is still in the box. The two electrons have identical properties, there are no marks on them that would let you distinguish one electron from the other. The uncertainty principle prevents you from tracking the particles. So when you detect one of the electrons, there is no way you can know which one you have detected. Composite particles in their ground states are also indistinguishable.
In practice we worry about indistinguishability when the particles are close enough together, so that their wave packets have an appreciable overlap. Two electrons in traps several km apart are very unlikely to tunnel through the wide barrier and exchange identities.
There are two categories of identical particles: bosons, which can share quantum states, defined by a unique set of quantum numbers, and fermions, which are forbidden from sharing a quantum state. This property of fermions is known as the Pauli exclusion principle. Examples of bosons are photons, gluons, phonons, and helium-4 atoms. Examples of fermions are electrons, neutrinos, quarks, protons and neutrons, and helium-3 atoms. (Composite particles made up of spin 1/2 particles, such as atoms made up of neutrons, protons, and electrons, are bosons if they contain an even number of spin 1/2 particles and fermions if they contain an odd number of spin 1/2 particles.)
The fact that particles can be identical has important consequences in statistical mechanics. Calculations in statistical mechanics rely on probabilistic arguments, which are sensitive to whether or not the objects being studied are identical. As a result, identical particles exhibit markedly different statistical behavior from distinguishable particles. The number of microstate consistent with a given macrostate can be very different for bosons, fermions, and distinguishable particle.
The macrostate of a system is its state as viewed at a macroscopic level. For instance, to describe the macrostate of an ideal gas in a cylinder, we could specify the number of gas molecules N in the cylinder, the total volume V of the cylinder, and total internal energy U of the gas molecules. As long as the gas is in internal thermal equilibrium, these three parameters suffice to determine its macrostate. Other thermodynamic variables, such as the temperature T and the pressure P of the gas, can then be calculated using the ideal gas law PV = NkBT and the relation U = (3/2)NkBT, where kB is the Boltzmann constant. In general, the macrostate of a system is characterized by the numbers and types of particles in the system and by internal parameters, such as mass, charge, and spin, by external physical constraints on the system such as volume, electric fields, and magnetic fields, and by conservation laws, such as energy conservation.
The microstate of a system is its state as viewed at the molecular level. In quantum mechanics a microstate is a particular quantum state of a system. To describe the microstate of the gas in the cylinder in classical mechanics, we have to specify the exact position and velocity of each individual molecule. In quantum mechanics we have to specify the quantum mechanical wave function of each molecule. If we know a systemís microstate, we also know its macrostate. On the other hand, knowing a systemís macrostate does not imply knowledge of its microstate.
The number of microstates that are consistent with a given macrostate is called the multiplicity Ω of that macrostate. The multiplicity is the number of accessible microstates, limited only by the constraints that determine the macrostate, i.e. it is the number of ways the insides of a system can be arranged so that from the outside things looks the same. For our gas in the cylinder, the multiplicity is a function of the three macroscopic variables N, V, and U. For most macrostates the multiplicity is a very large number, since there are an enormous number of different ways to distribute a given amount of energy among the systemís N molecules and to distribute the N molecules throughout the volume V.
The fundamental assumption of statistical mechanics is that an isolated system in equilibrium in a given macrostate is equally likely to be in any of its accessible microstates. This means that the probability of finding the system in any given microstate is 1/Ω, since there are Ω microstates, all equally probable. An isolated system is a system of fixed composition, fixed external parameters and fixed total energy. Equilibrium is the state in which the macroscopic properties are independent of time.
In-class activity: Macrostates and microstates
For a given macrostate, the number of available microstates differs for distinguishable particles, undistinguishable bosons and undistinguishable fermions. No two fermions can occupy the same quantum state, while bosons are even more likely than classical particles to share a quantum state. Let us work two simple problems to see how indistinguishability can affect the multiplicity of a macrostate.
Problem:
Assume that two particles are placed at random into one of two boxes. (The macrostate consist of two particles and two boxes.) Let a configuration be labeled by the number of particles in each box. There are only 3 configurations, shown below What are the probabilities of finding these distributions if the particles are classical particles, identical bosons, or identical fermions?
![]()
Classical particles are distinguishable. The state that has particle 1 in box 1 and particle 2 in box 2 differs from the state that has particle 2 in box 1 and particle 1 in box 2. Bosons and Fermions are indistinguishable. There is only one state with one of the indistinguishable particles in box 1 and the other in box 2. Fermions obey the Pauli exclusion principle. No two fermions can be in the same box.
Probability of finding a given distribution
|
|
|
|
|
| Classical | 1/4 | 1/2 | 1/4 |
| Boson | 1/3 | 1/3 | 1/3 |
| Fermion | 0 | 1 | 0 |
Problem:
Assume we have 3 states labeled a, b, and c, and 3 particles. Show that the probability of finding three identical bosons in the same state is larger than that of finding classical, distinguishable, particles in the same state. Determine the factor f by which this probability for bosons exceeds that for classical particles.
For classical particle there are 33
= 27 distinct arrangements. There are 3 ways we can put all three particles
in the same state. They can all be in the state a,
or in the state b, or in the
state g.
The probability of finding all three particles in the same state is 3/27 =
1/9.
For indistinguishable bosons, we can either put all 3 particles in the same
state (3 possibilities), or we can put 2 particles in the same state and one
particle into another state (3*(3-1) = 6 possibilities) or we can put each
particle in a different state (1 possibility). The total number of possible
arrangements is therefore 10. The probability of finding all the particles in
the same state is therefore 3/10.
f = (3/10)/(1/9) = 27/10 = 2.7.
Temperature
The particles that make up an object can have ordered energy and disordered energy. The kinetic energy of an object due to its motion with velocity v with respect to an observer is an example of ordered energy. The kinetic energy of individual atoms, when they are randomly vibrating about their equilibrium position, is an example of disordered energy. Thermal energy is disordered energy. The temperature is a measure of this internal, disordered energy.
The absolute temperature of any substance is proportional to the average kinetic energy associated with the random motion of the atoms or molecules that make up the substance.
In a gas, the individual atoms and molecules are moving randomly. The absolute temperature T of the gas is proportional to the average translational kinetic energy of a gas atom or molecule, Ĺm<v2>. In SI units, the proportional constant is (3/2)kB, where kB = 1.381*10-23 J/K or 1.381*10-23 Pa m3/K is called the Boltzmann constant.
Ĺm<v2> = (3/2)kBT
In a solid, the atoms can move randomly about their equilibrium positions. In addition, the solid as a whole can move with a given velocity and have ordered kinetic energy. Only the kinetic energy associated with the random motion of the atoms is proportional to the absolute temperature of the solid.
Assume we have a system of N particles in thermal equilibrium, with temperature T and total energy E, for example a cylinder of Volume V and temperature T containing a very large number N of molecules. There are many different ways the particles can share the total available energy, i.e. there are many different configurations. To each configuration correspond a large number of microstates. For a very large number N, the most probable configuration is so much more likely than any other configuration that the probability of observing it is essentially 1. In quantum mechanics the system has one-particle energy states labeled by a unique set of quantum numbers s. (For structureless particles in a 3D box, these quantum numbers s can be nx, ny, nz, with the ni being positive integers, ni = 1, 2, 3, ... .) The probability that we will find a particle in a particular one-particle energy state with energy Es is calculated by finding the number Ns of particles with energy Es for the most probable configuration. This number Ns depends on how many distinct microstates states are available for the most probable configuration and therefore can be very different for bosons, fermions, and distinguishable particles.
Distinguishable particles
For distinguishable particles the probability that a particle is in a particular state s with energy Es is proportional to exp(-Es/(kBT)).
P(Es) = Cexp(-Es/(kBT)).
C is the constant of proportionality. The factor exp(-E/(kT))
is called the Boltzmann factor.
Assume there are j possible states for the particle. The particle must
occupy one of those j states and therefore ΣjP(Ej)
must be equal to one.
ΣjP(Ej) = CΣjexp(-Ej/(kBT)) = 1, C = 1/Σjexp(-Ej/(kBT)) = 1/Z.
Z is called the partition function. It depends on how many distinct states are available for the particle. It therefore depends on the total number of particles N and the total energy E.
Bosons
Bosons are indistinguishable particles which have integer spin. The energy distribution of bosons is described by Bose-Einstein statistics. For a system containing a large number of bosons, the probability of finding a boson in a uniquely defined quantum state s with energy Es is given by
PBose-Einstein(Es) = 1/(Cexp((Es/kBT ) - 1).
For Es/kBT >> 1 the one in the denominator of
this expression can be neglected and PBose-Einstein(Es)
![]() exp(-Es/kBT).
But for Es/kBT >> 1 the Bose-Einstein
distribution is very different from the Boltzmann distribution. At very
low temperatures, when the total energy is very low, only individual particle
states with very low energies Es will be occupied. Bosons are
more likely than distinguishable particles to occupy the same low energy state
s.
exp(-Es/kBT).
But for Es/kBT >> 1 the Bose-Einstein
distribution is very different from the Boltzmann distribution. At very
low temperatures, when the total energy is very low, only individual particle
states with very low energies Es will be occupied. Bosons are
more likely than distinguishable particles to occupy the same low energy state
s.
Open the linked spreadsheet to explore the behavior of exp(-E/(kBT)) and 1/(exp((E/kBT ) - 1). as a function of E/kBT. (At very low temperatures the constant C in the above formula is very close to 1.) In quantum mechanics confinement leads to energy quantization. Often there are appreciable gaps between the lowest lying energy levels. Consider two adjacent energy levels, E1 and E2, E1 < E2. The difference between E1/kT and E2/kT gets bigger the lower the temperature. For bosons the probability of finding a boson in a state with near zero energy is much higher than finding it in a state whose energy is twice or three times as high. (See the spreadsheet! Compare probabilities E/(kT) = 0.01 and 0.04.)
Below a critical temperature TC, a large number of bosons is likely to occupy the lowest-lying single particle state or ground state. This is called condensation, or Bose-Einstein condensation. Since Ĺm<v2> = (3/2)kBT, the average deBrolie wavelength of the bosons, λ = h/p = h/√(2mE) = h/√(3mkBT) increases as the temperature decreases. Below the critical temperature TC, the deBrolie wavelength becomes larger than the average spacing between the bosons. The wave functions of all the bosons in the condensate overlap and form a superposition.
Condensation is responsible for the phenomenon of superfluidity in liquid helium. At very low temperatures (< 4.2 K) Helium liquefies. At a temperature 2.17 K, a part of the liquid becomes a "superfluid", a zero viscosity fluid which will move rapidly through any pore in the apparatus. A superfluid, placed in a closed loop, can flow endlessly without friction or drag. A vacuum container which seems to be leak tight can suddenly leak helium rapidly as the superfluid moves out through a microscopic hole. In 1938, F. London proposed a "two-fluid" model to explain the behavior of the liquid: normal liquid and the superfluid fraction consisting of those atoms which have "condensed" to the ground state. The normal component has all the properties associated with normal fluid, and the superfluid component has zero viscosity and infinite thermal conductivity. The atoms making up the superfluid all have exactly the same properties, since they are indistinguishable and their wave packets overlap forming one giant wave packet. It is impossible to set up a temperature gradient in a superfluid. (Particles stuck in the ground state cannot loose energy to the environment.) Recently in the field of chemistry, superfluid helium-4 has been successfully used in spectroscopic techniques, as a quantum solvent. A superfluid medium allows a molecule to have effective rotational freedom, allowing it to behave exactly as it would in the gas phase.
When Helium at a temperature below 2.17 K is locally heated, then the superfluid component flows towards the heated area. Heat causes superfluid to turn into normal fluid. A flow of superfluid into the heated area cools that area and restores the uniform mixture of the components. This flow can be observed via the fountain effect. To produce the fountain effect a chamber is connected to a reservoir of Helium below 2.17 K by a porous disc through which the superfluid component leaks easily, but through which the normal component cannot pass. If the interior of the chamber is heated, superfluid helium leaks through the disk and the pressure in the chamber increases, causing a liquid to fountain to spout from a small hole at the top.
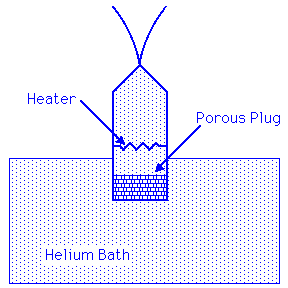

Links:
In 1924 Einstein pointed out that bosons could "condense" in unlimited numbers into a single ground state. Little notice was taken of this curious possibility until the anomalous behavior of liquid helium at low temperatures was studied carefully. In 1990 it was discovered that Bose-Einstein condensates could be formed with ultra-cold atoms.
The conditions for achieving a Bose-Einstein condensate are quite extreme. The participating particles must be considered to be identical, and this is a condition that is difficult to achieve for whole atoms. The condition of indistinguishability requires that the wave packets of the particles overlap significantly. The wave packets have roughly the width of the deBroglie wavelength. Indistinguishability requires extremely low temperatures so that the deBroglie wavelengths will be long, and it requires a fairly high particle density so that the average distance between particles is small.
The use of laser cooling and the trapping of ultra-cold atoms with magnetic traps has produced temperatures in the nano-Kelvin range. Cornell and Wieman along with Ketterle of MIT received the 2001 Nobel Prize in Physics "for the achievement of Bose-Einstein condensation in dilute gases of alkali atoms, and for early fundamental studies of the properties of the condensates". Cornell and Wieman led an active group at the University of Colorado, Boulder which has produced Bose-Einstein condensates with rubidium atoms. Other groups at MIT, Harvard and Rice have been very active in this rapidly advancing field.
The false-color images below display the velocity distribution of a cloud of rubidium atoms just before the appearance of the Bose-Einstein condensate (left), just after the appearance of the condensate (middle, and after further evaporation left a sample of nearly pure condensate (right). The field of view of each frame is 200 x 270 micrometers, and corresponds to the distance the atoms have moved in about 1/20 of a second. The color corresponds to the number of atoms at each velocity, with red being the fewest and white being the most. Areas appearing white and light blue indicate lower velocities.
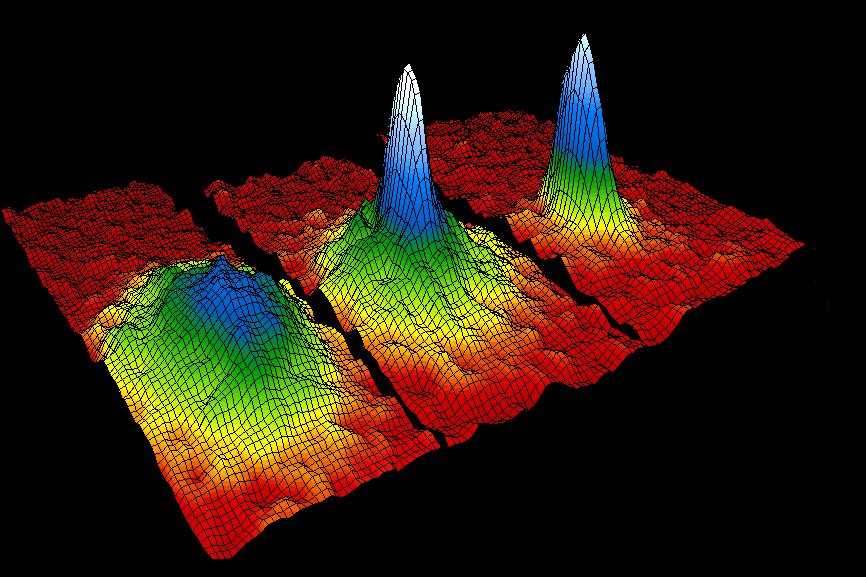
For more information please work through the Physics 2000 tutorial on Bose Einstein condensation at the Bec Homepage.
Bose-Einstein condensates are a first step towards an atom laser. An atom laser is analogous to an optical laser, but it emits matter waves instead of electromagnetic waves. Its output is a coherent matter wave, a beam of atoms which can be focused to a pinpoint or can be collimated to travel large distances without spreading. The beam is coherent, which means, for instance, that atom laser beams can interfere with each other. Compared to an ordinary beam of atoms, the beam of an atom laser is extremely bright. One can describe laser-like atoms as atoms "marching in lockstep". Although there is no rigorous definition for the atom laser, all people agree that brightness and coherence are the essential features.
Link:
Problem:
Indistinguishability requires extremely low temperatures so that the deBroglie wavelengths will be long, and it requires a fairly high particle density so that the average distance between particles is small. The expression found by Einstein relating the number density n to the critical temperature Tc at which a Bose Einstein condensate can form is
n = (2.32/(4π2))(2mkTc/ħ2)3/2,
where m is the mass of the bosonic atom. What is the density of 87Rb atoms for a critical temperature of 2*10-7 K?
Solution:
The mass of 87Rb is, to a good approximation, 87
times the mass of a nucleon, 1.67*10-27 kg.
Therefore
n = (2.32/(4π2))(2*87*1.67*10-27 kg*1.38*10-23 J/K*2*10-7 K/(1.055*10-34Js)2)3/2 = 3.6 *1019 atoms/m3.
Even though that is a large number, it is a very dilute gas. The density of air at standard temperature and pressure is about 3 *1025 atoms/m3.
Fermions
Fermions obey the Pauli exclusion principle. Fermions are forbidden to share a quantum state. Assume you want to put a large number N of spin 1/2 fermions with mass m into a 3-dimensional cubical box with sides of length L. The available energy levels in the box are
E = (nx2 + ny2 + nz2)π2ħ2/(2mL2), nx, ny, nz, = 1, 2, 3, ... .
Each energy level can be occupied by two particles, one with spin up and one with spin down. If the particles occupy the lowest energies allowed by the Pauli exclusion principle, then the highest filled energy level has energy
EF = (ħ2/(2m))(3π2n)2/3
Here n is the number density of the particles, the number per unit volume; n = N/V = N/L3. The energy EF is called the Fermi energy, and EF is proportional to V-2/3.
EF= AV-2/3, A = (ħ2/(2m))(3π2N)2/3
While the 3D cubical box is a system for which the Fermi energy can be calculated without too much difficulty, the Fermi energy is defined for any system of fermions as the highest filled energy level, when all the particles occupy the lowest energies allowed by the Pauli exclusion principle.
Not all fermions always occupy the lowest allowed energy states. The energy distribution of fermions is described by Fermi-Dirac statistics. For a system containing a large number of fermions, the probability of finding af fermions in a uniquely defined quantum state with energy Es is given by
PFermi-Dirac(Es) = 1/(exp((Es-EF)/kT) + 1).
At absolute zero, PFermi-Dirac(Es) = 1 for energies less than the Fermi energy and PFermi-Dirac(Es) = 0 for energies greater than the Fermi energy. All the levels up to the Fermi energy as filled, but no particle has a greater energy.
Use the linked spreadsheet to explore
the distribution at higher temperatures.
Note: A quantum state of a fermion gas with an energy equal to the Fermi
energy has a probability of 0.5 of being occupied.
Incompressibility of matter
The Pauli exclusion principle plays a crucial role in explaining the incompressibility of most solids.
To compress matter we have to exert a pressure P. A pressure is a force per unit area. If we exert a pressure P on an object and change its volume by an amount ∆V, we do an amount of work P∆V. The internal energy of the object increases by an amount ∆E = -P∆V. The pressure we exert on the object has magnitude P = |∆E/∆V|. We push inward on the object, and the object pushes outward with a pressure of equal magnitude.
Assume the electrons in the object act like the electrons in the cubical box. Then, as the volume decreases, the Fermi energy increases. The average energy of the electrons Eavg is approximately equal to (3/5)EFNe, so it also increases. This change in the average energy
|∆Eavg/∆V| = |(3/5)ANe dV-2/3/dV| = (2/5)ANeV-5/3 = (ħ2/(5m))(3π2)2/3n5/3
determines the pressure we have to exert to compress the object. It is called the degeneracy pressure Pdeg. This is a huge pressure. For copper, for example, we have Pdeg = 13.4*1010 N/m2. Atmospheric pressure is approximately 105 N/m2.
The exclusion principle also plays a critical part in the evolution of stars. It is responsible for preventing the collapse of a star that has used up all its nuclear fuel under the mutual gravitational attraction of its mass.
The electron degeneracy pressure has to offset the gravitational pressure, which for a star containing N nucleons of mass M is Pg = 0.32*G*(N*M)2/V4/3. When the electron degeneracy pressure equals the gravitational pressure equilibrium is reached. For a star with the mass of the sun this happens at a radius of about 7000 km, and at a density of approximately 7.5 metric tons per cubic centimeter. The normal radius of the sun is approximately 1.4 million km. When Pdeg = Pg, the collapsed star is called a white dwarf.
For stars with large masses, the Fermi energy we calculate using our non-relativistic equations becomes greater than the rest energy of the electron. We have to use relativistic equations. These equations are more complicated, and for stars with masses greater that 1.4 solar masses, the equation Pdeg = Pg can no longer be satisfied. There exist no solution. The degenerate pressure can no longer balance the gravitational pressure and the star continues to collapse. It becomes a neutron star or a black hole.