This is a many-body equation that cannot be solved exactly.  Approximations are necessary. 
In addition, we do not know the nuclear potential U(r₁,r₂,r₃, ...) very well.  It is mainly due to the strong nuclear force and the repulsive electrostatic Coulomb force.  But nucleons have spins and magnetic moments and since they are very close packed, magnetic interactions also become important.

Two approximations are often the starting point for calculation.  They are then refined by adding extra terms as small perturbations.

• We assume that the wave function can be separated into
  ψ(r₁,r₂,r₃, ..., t) = ψ₁(r₁, t)ψ₂(r₂, t)ψ₃(r₃, t). .. ,
  i.e. we assume that we can write the wave function as a product of single particle wave functions and that separation of variables is at least approximately possible.  Each particle then moves in an average potential created by the other particles.  Different approximations assume different shapes for this potential.  The simplest is a 3-dimensional spherical well.  In this well the neutron and protons behave like a Fermi gas, they fill the energy levels allowed by the Pauli exclusion principle.  We add deviations from the average interactions between the nucleons as perturbations.
   
• We assume that separation of variables is not possible.  We treat the nucleus as one single quantum-mechanical particle.  We then have again a one-body problem.  But the particle is not a point particle, it can change shape.  The wave function now must describe the shape of the particle and the potential energy of the particle depends on its shape.  If the nucleus deforms, the potential energy of the nucleus changes.  The kinetic energy is that of a rotating and vibrating object.

So there are two basic types of simple nuclear models.

• An individual particle model with nucleons in discrete energy states: Examples are the Fermi Gas Model or the Shell Model.

  The Shell Model (developed by Maria Goeppert-Mayer and Hans Jensen), emphasizes the orbits of individual nucleons in the nucleus.  The Nuclear Shell Model is similar to the atomic model where electrons arrange themselves into shells around the nucleus.  The atomic shell structure is due to the quantum nature of electrons and the fact that electrons are fermions.  Since protons and neutrons are also fermions, the energy states of the nucleons are filled from the lowest to the highest as nucleons are added to the nucleus.  In the shell model the nucleons fill each energy state with nucleons in orbitals with definite angular momentum.  There are separate energy levels for protons and neutrons.

  

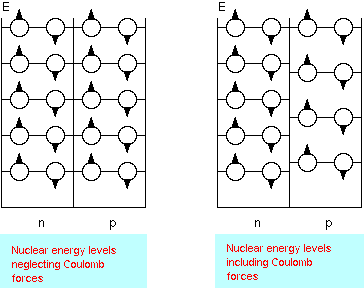
  The ground state of a nucleus has each of its protons and neutrons in the lowest possible energy level.  Excited states of the nucleus are then described as promotions of nucleons to higher energy levels.  This model has been very successful in explaining the basic nuclear properties.  As is the case with atoms, many nuclear properties (angular momentum, magnetic moment, shape, etc.) are dominated by the last filled or unfilled valence level.

  The nuclear shell model explains the existence of "magic numbers".  Nuclei with magic neutron number N = 2, 8, 20, 28, 50, 82, 126 or magic proton number Z = 2, 8, 20, 28, 50, 82 have a larger binding energy per nucleon than neighboring nuclei, and when N and Z are both magic the binding energy per nucleon is especially large.  This suggests a shell structure, similar to the shell structure in atomic physics, where the noble gases have especially large ionization energies.

  What is the origin of this shell structure?  Consider a single nucleon in a nucleus.  All the nucleons form a nuclear "fluid".  Our single nucleon interacts with all the other nucleons, but  the interactions change quickly and only treating the attraction of all the other nucleons as a function of position is a good approximation.  We postulate an average nuclear potential as shown in the figure below.

  

  The 3-dimensional spherical well or the isotropic three-dimensional harmonic oscillator potential allow analytical solutions.  Let us consider the three-dimensional harmonic oscillator potential.  The time-independent Schroedinger equation for this system is

  (-ħ²/(2m))Ѳψ(r,t) + (1/2)mω²r²ψ(r,t)  = Eψ(r,t),

  Seperation of variables is possible in Cartesian as well as in spherical coolrdinates.  Expressed in spherical coordinates, the eigenfunctions and eigenvalues of this system are

  ψ(r,t) = R_nl(r)Y_lm(θ,ϕ),  E_nl = (2n + l + 3/2)ħω,

  with n = 0, 1, 2, 3, ..., and l = 0, 1, 2, ... .
  Using Cartesian coordinates we write the eigenvalues as

  E_{nx, ny, nz} =  E_nl = (n_x + n_y + n_z + 3/2)ħω,  n_x, n_y, n_z =  0, 1, 2, ... .

  
  This simple model generates the first three magic numbers.

  

  The model fails for the larger magic numbers because it neglects the spin-orbit energy, which splits the levels by an amount which increases with orbital quantum number.
   

• A collective model with no individual particle states:  An example is the Liquid Drop Model which is the basis of the semi-empirical mass formula.
  • The Liquid Drop Model treats the nucleus as a liquid.  (The nuclear force is attractive unless the nucleons are squeezed close together.  A similar attractive/repulsive behavior characterizes the force between molecules.)   Nuclear properties, such as the binding energy, are described in terms of volume energy, surface energy, compressibility, etc, parameters that are usually associated with a liquid.  This model has been successful in describing how a nucleus can deform and undergo fission.
  
  The liquid drop model gives rise to the semi-empirical binding energy formula.  This formula is an approximate expression for the binding energy B(Z,N) of a nucleus.  Physical principles lead to various terms in the expression, but the coefficients come from measurements.

  B(Z,N) = C₁A - C₂A^2/3 - C₃Z(Z-1)/A^1/3 - C₄(N-Z)²/A.

  The liquid drop model of the nucleus takes into account that the forces on the nucleons on the surface are different from those on nucleons in the interior, where they are completely surrounded by other attracting nucleons.  This is similar to considering the surface tension to be a contributor to the energy of a tiny liquid drop.  The first term of the semi-empirical formula is the volume term.  It is proportional to the mass number A.  If we divide by A, this term alone would gives a constant prediction for B(Z,N)/A, which for large nuclei is nearly, but not completely, correct. 
  The second term in the formula is the surface term, which is proportional to A^2/3.  It decreases the binding energy because nucleons near the surface of the nucleus are in a less deep potential well.  The surface term is most important for the binding energy of small nuclei, because the ratio of the second to the first term is largest for small A.
  The third term of the semi-empirical formula is the Coulomb term.  Each pair of protons contributes to the Coulomb term equally.  The number of protons is Z, so the number of proton pairs is Z(Z-1)/2.  The electrostatic potential energy is proportional to the inverse distance.  The average inverse distance increases with the radius of the nucleus and therefore is proportional to A^1/3.  The total electrostatic potential energy term is proportional to Z(Z-1)/A^1/3, and it deceases the binding energy. 
  The fourth term of the formula expresses the fact that the binding energy decreases if a neutron is transformed into a proton, if the number of protons is larger than that of the neutrons.  The same holds if a proton is transformed into a neutron.

  With increasing Z the magnitude of the Coulomb term increases at the highest rate.  For some value of Z the magnitude of the Coulomb term will become larger than the volume term and the nucleus will become completely unstable.  No nuclei with Z > 120 can exist.  This is a direct consequence of the long range nature of the Coulomb force.

  • The Collective Model (developed by Aage Bohr and Ben Mottleson), extends the liquid drop model by including motions of the whole nucleus such as quantized rotations and vibrations.  The Collective Model emphasizes the coherent behavior of all of the nucleons.  Among the kinds of collective motion that can occur in nuclei are rotations or vibrations that involve the entire nucleus.  In this respect, the nuclear properties can be analyzed using the same description that is used to analyze the properties of a charged drop of liquid suspended in space.  The Collective Model can thus be viewed as an extension of the Liquid Drop Model.  Like the Liquid Drop Model, the Collective Model provides a good starting point for understanding fission.
    In addition to fission, the Collective Model has been very successful in describing a variety of nuclear properties, especially energy levels in nuclei with an even number of protons and neutrons.  These even nuclei can often be treated as having no valence particles.  These energy levels show the characteristics of rotating or vibrating systems expected from the laws of quantum mechanics.  Commonly measured properties of these nuclei, such as excited state energies, angular momentum, magnetic moments, and nuclear shapes, can be understood using the Collective Model.

The Shell Model and the Collective Model represent the two extremes of the behavior of nucleons in the nucleus.  More realistic models, known as unified models, attempt to include both shell and collective behaviors.