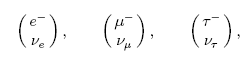The four fundamental interactions or forces that govern the behavior of
elementary particles are listed below.
- The strong force (It holds the nucleus together.)
- The electromagnetic force (It causes interactions between
charges.)
- The weak force (It causes beta decay.)
- The gravitational force (It causes interaction between states with energy.)
A given particle may not necessarily be subject to all four interactions.
Neutrinos, for example, experience only the weak and gravitational interaction.
The fundamental particles may be classified into groups in several ways.
First, all particles are classified into fermions,
which obey Fermi-Dirac statistics and bosons,
which obey Bose-Einstein statistics. Fermions have half-integer spin,
while bosons have integer spin. All the fundamental fermions have spin
1/2. Electrons and nucleons are fermions with spin 1/2. The
fundamental bosons have mostly spin 1. This includes the photon. The
pion has spin 0, while the graviton
has spin 2. There are also three particles, the W+, W−
and Z0 bosons, which are spin 1. They are the carriers of the
weak interactions.
We can also classify the particles according to their interactions.
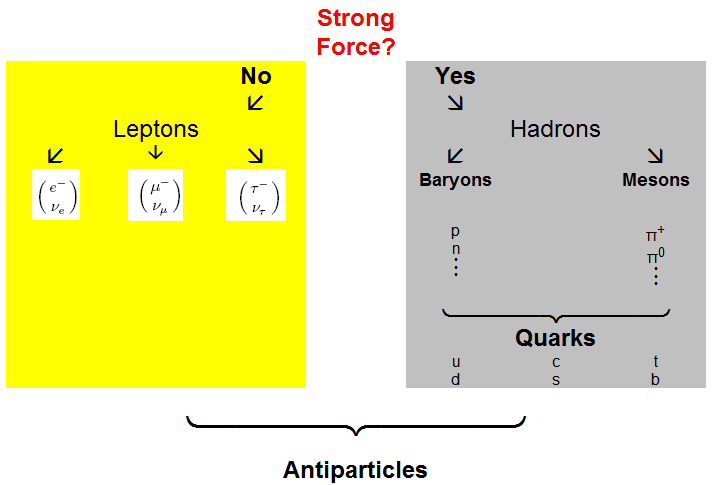
The electron and the neutrino are members of a family of
leptons. Originally leptons meant
"light particles", as opposed to baryons, or
heavy particles, which referred initially to the proton and neutron. The
pion, or pi-meson, and another particle called the muon or mu-meson, were called
mesons, or medium-weight particles, because
their masses, a few hundred times heavier than the electron but six times
lighter than a proton, were in the middle. But that distinction turned out
not to be very useful. We now recognize the muon to be almost the same as
an electron, and the leptons now consist of three "generations" of pairs of
particles,
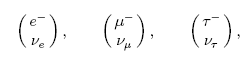
with the heaviest of these, the tau lepton τ−,
being almost twice as massive as the proton
The leptons are distinguished from other particles called hadrons in that
leptons do not participate in strong interactions. The bottom lepton
in each of the three "doublets" shown above is not only neutral, but also
has a very small mass. Neutrinos had been considered massless for many
years, but more recent experiments have shown their mass to be non-zero.
Table of leptons
| particle |
associated neutrino
|
Name
|
Charge
(e) |
Mass
(MeV) |
Name |
Charge
(e) |
Mass
(MeV) |
| Electron (e-) |
-1 |
0.511 |
Electron neutrino (νe) |
0 |
< 0.000003 |
| Muon (μ-) |
-1 |
105.6 |
Muon neutrino (νμ) |
0 |
< 0.19 |
| Tau (τ-) |
-1 |
1777 |
Tau neutrino (ντ)
|
0 |
< 18.2 |
Hadrons are strongly interacting
particles. They are divided into baryons
and mesons. The baryons are a class of
fermions, including the proton and neutron, and other particles which in a decay
always produce another baryon, and ultimately a proton. The mesons, are bosons. In addition to the pion, there are other spin 0 particles, four kaons and two eta mesons, and a
number of spin one hadrons, including the three rho mesons, which like the pion
come in charges 1 and 0. Mesons can decay without necessarily producing
other hadrons.
Table of some baryons
Particle
|
Symbol
|
Quark
Content |
Mass
MeV/c2 |
Mean
lifetime (s) |
Decays to
|
| Proton |
p |
uud |
938.3 |
Stable |
Unobserved |
| Neutron |
n |
ddu |
939.6 |
885.7±0.8 |
p + e- +
νe |
| Delta |
Δ++ |
uuu |
1232 |
6×10-24 |
π+ + p |
| Delta |
Δ+ |
uud |
1232 |
6×10-24 |
π+ + n
or π0 + p |
| Delta |
Δ0 |
udd |
1232 |
6×10-24 |
π0 + n
or π- + p |
| Delta |
Δ- |
ddd |
1232 |
6×10-24 |
π- + n |
| Lambda |
Λ0 |
uds |
1115.7 |
2.60×10-10 |
π- + p
or πo + n |
| Sigma |
Σ+ |
uus |
1189.4 |
0.8×10-10 |
π0 + p
or π+ + n |
| Sigma |
Σ0 |
uds |
1192.5 |
6×10-20 |
Λ0 + γ |
| Sigma |
Σ- |
dds |
1197.4 |
1.5×10-10 |
π- + n |
| Xi |
Ξ0 |
uss |
1315 |
2.9×10-10 |
Λ0 + π0 |
| Xi |
Ξ- |
dss |
1321 |
1.6×10-10 |
Λ0 + π- |
| Omega |
Ω- |
sss |
1672 |
0.82×10-10 |
Λ0 + K-
or Ξ0 + π- |
Table of some mesons
Particle
|
Symbol
|
Anti-
particle |
Quark
Content |
Mass
MeV/c2 |
Mean
lifetime (s) |
Principal
decays |
| Charged
Pion |
π+ |
π− |
ud |
139.6 |
2.60×10-8 |
μ+ +
νμ |
| Neutral
Pion |
π0 |
Self |
uu
- dd |
135.0 |
0.84×10-16 |
2γ |
| Charged
Kaon |
K+ |
K− |
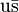 |
493.7 |
1.24×10-8 |
μ+ +
νμ
or π+ + π0 |
| Neutral
Kaon |
K0 |
K0 |
ds |
497.7 |
|
|
| Eta |
η |
Self |
uu
+ dd
- 2ss |
547.8 |
5×10-19 |
|
| Eta
Prime |
η' |
Self |
uu
+ dd
+ ss |
957.6 |
3×10-21 |
|
Each elementary particle is associated with
an antiparticle with the
same mass and opposite charge. Some particles, such as the
photon, are identical to their antiparticle. Such
particles must be neutral, but not all neutral particles are
identical to their antiparticle. Particle-antiparticle
pairs can annihilate each other if they are in appropriate
quantum states, releasing an amount of energy equal to twice
the rest energy of the particle. They can also be produced in various
processes, if enough energy is available. The minimum
amount of energy needed is twice the rest energy of the
particle, if momentum conservation allows the
particle-antiparticle pair to be produced at rest.
Most often the antiparticle is denoted by the same symbol as
the particle, but with a line over the symbol.
For example, the antiparticle of the proton p, is denoted by
p.
Protons and neutrons are made of still
smaller particles called quarks. At
this time it appears that the two basic constituents of matter are the leptons
and the quarks. There are believed to be six types of each.
Each quark type is called a flavor, there are six quark
flavors. Each type of lepton and quark also has a corresponding
antiparticle, a particle that has the same mass but opposite
electrical charge and magnetic moment. An isolated quark has never been
found, quarks appear to almost always be found in pairs or triplets with other
quarks and antiquarks. The resulting particles are the hadrons, more than
200 of which have been identified. Baryons are made up of 3 quarks, and
mesons are made up of a quark and an anti-quark. Baryons are fermions and
mesons are bosons. Two theoretically predicted five-quark
particles, called pentaquarks, have been produced in the laboratory. Four-
and six-quark particles are also predicted but have not been found.
The six quarks have been named up, down, charm, strange, top, and
bottom. The top quark, which has a mass greater than an entire
atom of gold, is about 35 times more massive than the next biggest quark and may
be the heaviest particle nature has ever created. The quarks found in
ordinary matter are the up and down quarks, from which protons and neutrons are
made. A proton consists of two up quarks and a down quark, and a
neutron consists of two down quarks and an up quark. The pentaquark consists of
two up quarks, two down quarks, and the strange antiquark. Quarks have
fractional charges of one third or two thirds of the basic charge of the
electron or proton. Particles made from quarks always have integer charge.
Table of Quarks
Name
|
Symbol
|
Charge
(e) |
Spin
|
Mass
MeV/c2 |
Strangeness
|
Baryon
number |
Lepton
number |
| up |
u |
+2/3 |
1/2 |
1.7-3.3 |
0 |
1/3 |
0 |
| down |
d |
-1/3 |
1/2 |
4.1-5.8 |
0 |
1/3 |
0 |
| strange |
s |
-1/3 |
1/2 |
101 |
-1 |
1/3 |
0 |
| charm |
c |
+2/3 |
1/2 |
1270 |
0 |
1/3 |
0 |
| bottom |
b |
-1/3 |
1/2 |
4190-4670 |
0 |
1/3 |
0 |
| top |
t |
+2/3 |
1/2 |
172000 |
0 |
1/3 |
0 |
In the current theory, known as the Standard Model there are 12 fundamental
matter particle types and their corresponding antiparticles. In addition,
there are gluons, photons, and W and Z bosons, the force carrier particles that
are responsible for strong, electromagnetic, and weak interactions respectively.
These force carriers are also fundamental particles.

All we know is that quarks and leptons are smaller than 10-19
meters in radius. As far as we can tell, they have no internal structure
or even any size. It is possible that future evidence will, once again,
show our understanding to be incomplete and demonstrate that there is
substructure within the particles that we now view as fundamental.
The Discovery of Elementary Particles
The first subatomic particle to be discovered was the electron, identified in
1897 by J. J. Thomson. After the nucleus of the atom was discovered in
1911 by Ernest Rutherford, the nucleus of ordinary hydrogen was recognized to be
a single proton. In 1932 the neutron was discovered. An atom
was seen to consist of a central nucleus containing protons and neutrons,
surrounded by orbiting electrons. However, other elementary particles not
found in ordinary atoms immediately began to appear.
In 1928 the relativistic quantum theory of P. A. M. Dirac predicted the
existence of a positively charged electron, or positron, which is the
antiparticle of the electron. It was first detected in 1932.
Difficulties in explaining beta decay led to the prediction of the neutrino in
1930, and by 1934 the existence of the neutrino was firmly established in
theory, although it was not actually detected until 1956. Another
particle was also added to the list, the photon, which had been first suggested
by Einstein in 1905 as part of his quantum theory of the photoelectric effect.
The next particles discovered were related to attempts to explain the strong
interactions, or strong nuclear force, binding nucleons together in an atomic
nucleus. In 1935 Hideki Yukawa suggested that a meson, a charged
particle with a mass intermediate between those of the electron and the proton,
might be exchanged between nucleons. The meson emitted by one nucleon would be
absorbed by another nucleon. This would produce a strong force between the
nucleons, analogous to the force produced by the exchange of photons between
charged particles interacting through the electromagnetic force. It
is now known that the strong force is mediated by the gluon. The following
year a particle of approximately the required mass, about 200 times that of the
electron, was discovered and named the mu-meson, or muon. However, its
behavior did not conform to that of the theoretical particle. In 1947 the
particle predicted by Yukawa was finally discovered and named the pi-meson, or
pion. Both the muon and the pion were first observed in cosmic rays.
Further studies of cosmic rays turned up more particles. By the 1950s
these elementary particles were also being observed in the laboratory as a
result of particle collisions in particle accelerators.
By the early 1960s over 30 "fundamental particles" had been found. A rigorous
way of classifying them was needed. Were there any symmetries or patterns?
Murray
Gell-Mann believed that a framework for such patterns could be found in the
mathematical structure of groups. A symmetry group called SU(3) offered
patterns he was looking for. In 1961, after grouping the known particles, he
predicted the existence of the η particle which was needed
to complete a pattern. The η particle was discovered a few months later.
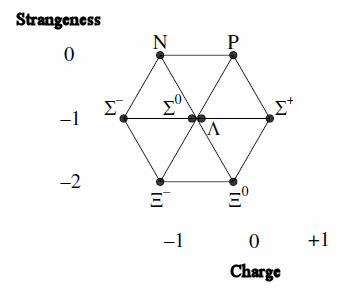
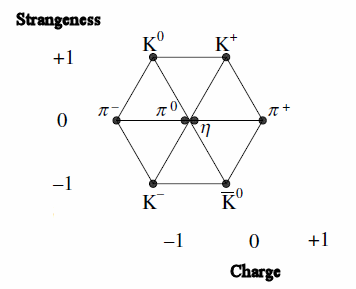
Example patterns for some baryons and mesons (The Eightfold Way)
After finding the patterns an explanation was needed. In 1964 Gell-Mann
published a short article showing that the patterns could be produced if the
known particles were viewed as combinations of 3 fundamental subunits with
fractional charge, the up, down, and strange quarks and their antiquarks. There
were however problems with the Pauli Exclusion Principle. The quarks are spin
1/2 fermions and the Δ++(uuu) and the Ω-(sss) seemed to
contain at least two quarks with exactly the same quantum numbers. The quark
theory was not really accepted until
deep inelastic scattering experiments revealed structure inside the protons
in the later 1960s.
The charm quark was discovered in 1974, the
bottom quark in 1977, and the top quark in 1995. The tau particle was detected in a
series of experiments between 1974 and 1977 and the discovery of the tau neutrino was
announced in 2000. It was the last of the
particles in the Standard Model of elementary particles to be detected.
One of the current frontiers in the study of elementary particles concerns the
interface between that discipline and cosmology. The known quarks and leptons,
for instance, are typically grouped in three families, where each family
contains two quarks and two leptons. Investigators have wondered whether
additional families of elementary particles might be found. Recent work in
cosmology pertaining to the evolution of the universe has suggested that there
could be no more families than four, and the cosmological theory has been
substantiated by experimental work at the Stanford Linear Accelerator and at
CERN, which indicates that there are no families of elementary particles other
than the three that are known today. For
example, detailed studies of Z0
decays at CERN revealed that there can be no more than three different kinds of
neutrino. If there was a fourth, or a fifth, further decay routes would be open
to the Z0 which would affect its measured lifetime.
Conservation Laws
Leptons carry an additive quantum number called the
lepton number L. The leptons listed in the table above carry L
= 1 and their antiparticles carry L = -1. The
electron number carried by electrons and electron neutrinos
seems to an additive quantum number which is conserved in interactions. Electrons and
electron neutrinos have electron number 1 and positrons and electron
anti-neutrinos carry electron number -1. Muons, or μ-mesons,
behave similarly as electrons. They only have electromagnetic and weak
interactions. Only their mass, 106 MeV/c2, distinguishes them
from electrons. Along with νμ they carry an additive quantum number, the
muon number, that which also seems to be conserved in interactions. Muons decay as
μ+ -->
e+ + νμ
+ νe
in about 10-6s. The tau and its neutrino carry an
additive quantum number as well, which seems to be conserved in interactions.
We say that the lepton family number LF also
seems to be conserved. However if neutrinos have mass and can change flavor,
for example, if muon neutrinos can change into
electron neutrinos and vice versa, then only L is conserved.
Are there more such additive quantum numbers? Yes, there is a group of
particles called baryons, and a corresponding conserved quantum number called
baryon
number B. Baryons have
baryon number B = 1 and anti-baryons have baryon number B = -1. The lightest baryon is
the proton, and it is the only stable baryon. Since the neutron decays by
n --> p + e - +
νe
and the electron and anti-neutrino are leptons, not baryons,
B conservation requires that the neutron
is also baryon.
It is fairly easy to spot a baryon in a table of elementary particles.
Suppose you are looking at a particle which might be a baryon. If it is
not the proton and it is a baryon, it must decay. Baryon conservation then
requires a baryon among the decay products, although you may not know which of
the decay products is the baryon. Let all of the decay products themselves
decay. The baryon's decay yields another baryon. Keep going until
all the particles are stable. Among all the resulting particles there must
be one net baryon. Since the proton is the only stable baryon, that baryon
must be a proton. Hence, a particle is a baryon if and only if there is
one net proton among its ultimate decay products.
Baryons are made up of 3 quarks. All quarks have baryon number B = 1/3,
and all anti-quarks have baryon number B = -1/3.
Everything else in the table besides the baryons and leptons is called a meson.
Mesons are made up of a quark and an anti-quark. Mesons have L = 0 and B = 0, and they have no net leptons or baryons in their
ultimate decay products. The number of mesons is not conserved, so there
is no "meson number."
After the discovery of pions other particles were discovered in rapid pace.
K-mesons (m = 494 MeV/c2) are similar to π -mesons, they do not carry a nucleon number. The K-meson
decays in the following way.
K+ --> π+ +
π0
Hyperons are different. The lightest hyperon is the Λ0 with m = 1116 MeV/c2.
It decays in the following way
Λ0 -->
p + π-, or n +
π0
A hyperons is a baryon.
As better accelerators became available the reaction below was observed
π+
+ n --> Λ0 + K+
Obviously in the above process baryon number is conserved. It was
remarkable that reactions like
π+
+ n --> Λ0 +
π +
were never observed. This prompted the introduction of a new quantum
number, strangeness, by Gell-Mann and Pais.
The strangeness S(Λ0)
= -1, S(K+) = 1. Protons, neutron an pions have no
strangeness. In decay processes involving the strong interaction
strangeness is conserved. In decay processes involving the weak
interaction, such as K-decay or hyperon decay, strangeness is not conserved.
This was the first case that some quantum numbers were conserved in strong
interactions and electromagnetic interactions, but not in weak interactions. Decay processes governed by the strong interaction can be distinguished easily from decay
processes governed by the weak interaction. Characteristic reaction times for
the former are on the order of 10-23 s while for the latter they are
on the order of 10-10 s.
Problems:
Determine whether a stationary proton can decay according to the scheme p -->
π0 +
π+.
- Solution:
We have to check whether the decay violates any of the conservation laws.
- Energy conservation:
Q = minitialc2 - mfinalc2 =
mprotonc2 - (mπ0c2
+ mπ+c2)
= (938.3 - (135.0 + 139.6))MeV = 663.7 MeV.
Energy conservation is not violated, the proton has enough mass to decay
into the pair of pions.
- Momentum conservation:
Momentum can be conserved if the two pions move in opposite directions
after the decay.
- Angular momentum conservation:
The proton is a spin 1/2 particle (fermion), the pions are spin 0
particles (bosons).
The orbital angular momentum quantum number can only be an integer, so
there is no way that angular momentum can be conserved. The
proposed decay cannot occur.
- The decay also violates conservation of Baryon number. The
proton has B = 1 and the pions both have B = 0.
A Xi-minus particle decays in the following way: Ξ-
--> Λ0 + π-. The lambda-zero
and the pi-minus particles are both unstable. The following processes
occur in a cascade, until only relatively stable products remain.
Λ0 --> p + π-, π-
--> μ- +
νμ,
μ- --> e- +
νμ +
νe.
(a) Is the Xi-minus particle a lepton or a hadron? If the
latter, is it a baryon or a meson?
(b) Does the decay process conserve the three lepton numbers?
- Solution:
(a) Only three families of leptons exist and none includes the the
Xi-minus. It must be a hadron.
The final decay products are p + 2(e- +
νμ +
νμ +
νe),
since two pi-minus particles decay. The baryon number of the proton is
1 and the baryon number of all the other particles is zero. The net
baryon number therefore is 1 and the Xi-minus is a baryon.
(b) The proton has lepton number zero, the electron has electron
lepton number 1, the anti-electron neutrino has electron lepton number -1,
the muon neutrino has muon lepton number 1, and its antiparticle has muon
lepton number -1. All lepton numbers add up to zero after the decay,
and they are zero before the decay, since the Xi-minus is a baryon. The
decay process conserves the three lepton numbers.
The Xi-minus particle has spin quantum number s = 1/2, charge q = -e, and
strangeness quantum number S = -2. It does not contain a bottom quark.
What combination of quarks is it made of?
- Solution:
The Xi-minus particle is a baryon, it is made up of three quarks. It
must contain two strange quarks to have S = -2. This yields a charge
of -(2/3)e. We must add another quark with S = 0 and charge -(1/3)e.
Since the b-quark is excluded, we must add a d-quark. The quark
combination for the Xi-minus is dss.
Link: