Assume a Stern-Gerlach type experiment is performed with an apparatus as shown in the figure.

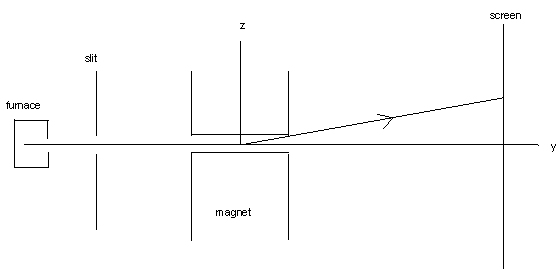
A beam of silver atoms emerges from a furnace held at 1000 K.  It is collimated using 0.1 mm slits, passed between the poles of a magnet, and directed onto a screen, where the atoms are detected.  The speed of the silver atoms is approximately 500 m/s (from (3/2)kT = ½mv²), k = 1.38*10^-23 J/K).  Assume the apertures collimate the beam to approximately 0.1^o angular spread.  The spread in the component of velocity perpendicular to the beam direction is at least 1 m/s since Δv_z = (500 m/s)*sin(0.1^o).  We have  Δv_zΔz ≥ 10^-4 m²/s.  The uncertainty principle requires that  Δv_zΔz ≥ ħ/M ≈ 10^-10 m²/s.  (M_silver = 1.6*10^-27 kg * 108.)  The position and momentum of a particle must be treated quantum-mechanically when Δp_iΔr_i approaches the minimum value required by the uncertainty principle.  In a typical Stern-Gerlach type experiment this is not the case.  The external degrees of freedom of the silver atoms can be treated classically.  The dimensions of the wave packet are much smaller that the characteristic dimensions of the problem.

Assume each silver atom has a permanent magnetic moment m.  We assume that m = γS, where S denotes the intrinsic angular momentum of the silver atom.  γ is called the gyromagnetic ratio.  If m is a fundamental property of the atom, then its total energy in an external magnetic field is W = -m∙B.  The torque on the atom is τ = m×B, and the force is F = ∇(m∙B).

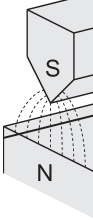
In our experiment B = (Bx, 0, Bz) is an inhomogeneous field.  In the region of interest, where the beam passes through the field, we have Bz >> Bx,  B ≈ Bk.  Therefore τ = m×Bk, τ = dS/dt = γS×Bk. dSx/dt = γBzSy,  dSy/dt = -γBzSx,  dSz/dt = 0. The component Sz is constant, while the component perpendicular to the z-axis rotates about the z-axis.

Consider an arbitrary vector A, rotating cw about the origin in the x-y plane with angular velocity ω = dθ/dt.

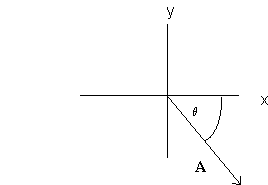
A_x = Acosθ, A_y = -Asinθ, 
dA_x/dt = (dA_x/dθ)(dθ/dt) = -Asinθω,   dA_y/dt = (dA_y/dθ)(dθ/dt) = -Acosθω.
dA_x/dt = ωA_y,  dA_y/dt = -ωA_x.
S_⟂ rotates about the z-axis with angular velocity ω = |γB_z|.  For positive γB_z it rotates cw, and for negative γB_z it rotates ccw.

The z-component of F acting on the silver atoms is
F_z = ∂/∂z(m_zB_z + m_xB_x) ≈ ∂/∂z(m_zB_z) = m_z∂B_z/∂z.
F_z produces a deflection of the atoms in the z-direction which is proportional to m_z.  If ∂B_z/∂z is known, then measuring this deflection is equivalent to measuring m_z.
Classically, we expect to find all values of m_z between m_z = +|m| and m_z= -|m|.
In the experiment the silver atoms hit the screen in two distinct spots.  The measurement yields only two possible values for m_z.  S_z is therefore a quantized observable, whose discrete spectrum has only two eigenvalues, which we will find to be ±ħ/2.

In quantum mechanics, every measurable physical quantity is associated with a Hermitian operator whose eigenvectors form a basis for the state space.  Assume that S_z is the observable associated with the z-component of the spin.  The state space corresponding to the observable S_z of a Silver atom (a spin ½ particle) is therefore two-dimensional. 
We denote the eigenvectors of S_z by |+> and |->.
S_z|+> = (ħ/2)|+>,  S_z|-> = -(ħ/2)|->.
We assume that the eigenvectors are normalized.
<+|+> = <-|-> = 1,  <+|-> = 0.
S_z alone is a C.S.C.O. in the state space E_spin spanned by the vectors |+> and |->.  The closure relation is written as |+><+| + |-><-| = I.
The most general element of E_spin is |ψ> = a|+> + b|->.  If <ψ|ψ> = 1, then |a|² + |b|² = 1.
The matrix of S_z in the {|+>, |->} basis is

 .

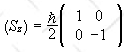The complete state space for a particle is E = E_space ⊗ E_spin.  However, if in a given problem the spatial degrees of freedom can be treated classically, then we can predict the outcome of measurements which depend on the internal degrees of freedom by considering only the state vector in E_spin.

Let S_x and S_y denote the observables associated with the x- and y-components of the spin of a spin ½ particle, and S_u = S∙u the observable associated with the component along a direction defined by the unit vector u .  E_spin can also be spanned by the eigenvectors |±>_x of S_x, |±>_y of S_y, or |±>_u of S_u.  However, S_x, S_y, and S_z do not commute, they are incompatible observables.  The eigenvectors of S_i are not eigenvectors of S_j and S_k.  The matrices of S_x and S_y in the eigenbasis of S_z , {|+>, |->}, are not diagonal.  Theoretical predictions agree with observations if (S_x) and (S_y) in the {|+>, |->} basis are given by

,  .

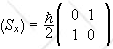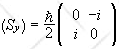We write S = (ħ/2)σ. The matrices of the three components of σ in the {|+>, |->} basis are called the Pauli matrices.

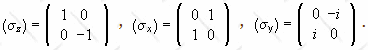
The eigenvalues of σ_x and σ_y are ±1.
The eigenvectors of σ_x are |±>_x = (1/√2)(|+> ± |->),
and the eigenvectors of σ_y are |±>_y = (1/√2)(|+> ± i|->).
These are also the eigenvectors of S_x and S_y .

Properties of σ_x and σ_y and σ_z

• det(σ_i) = -1,  Tr{σ_i} = 0,  σ_i² = I,  σ_xσ_y = -σ_yσ_x = iσ_z.
  In general, σ_iσ_j =  iε_ijkσ_k + δ_ijI,   [σ_i,σ_j] = i2ε_ijkσ_k.
  Therefore 
  [S_x,S_y] = iħS_z,   [S_y,S_z] = iħS_x,    [S_z,S_x] = iħS_y,
  since S = (ħ/2)σ.  We have already shown that [J_i,J_j] = iħε_ijkJ_k are commutation relations for angular momentum.
  The Pauli matrices anti-commute, (σ_iσ_j + σ_jσ_i) = 0.  We also find σ_xσ_yσ_z = iI.

• Any arbitrary 2 by 2 matrix can be written as a linear combination of the four matrices σ_x, σ_y, σ_z and I.

  Let    be an arbitrary 2 by 2 matrix.
  M = ½(m₁₁ + m₂₂)I + ½(m₁₁ - m₂₂)σ_z + ½(m₁₂ + m₂₁)σ_x + (i/2)(m₁₂ - m₂₁)σ_y
  = a₀I + a_zσ_z + a_xσ_x + a_yσ_y.
  (M) is a Hermitian matrix if a₀, a_x, a_y, and a_z are real.
  a₀ = ½Tr{M},  a = ½Tr{Mσ}.

The operator S_u is defined through S∙u = S_xsinθcosφ + S_ysinθsinφ + S_zcosθ.
The matrix of S_u is (S_u) = (S_x)sinθcosφ + (S_y)sinθsinφ + (S_z)cosθ

= .

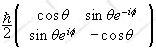The eigenvectors of S_u are
|+>_u = cos(θ/2)exp(-iφ/2)|+> + sin(θ/2)exp(iφ/2)|->,
|->_u = -sin(θ/2)exp(-iφ/2)|+> + cos(θ/2)exp(iφ/2)|->.

The most general normalized ket in the spin state space E_spin is |ψ> = a|+> + b|->, |a|² + |b|² = 1.  |ψ> is the eigenvector of some operator S_u with eigenvalue ±ħ/2.  There exists a unit vector u and an operator S_u such that |ψ> =|+>_u.  An arbitrary state vector can be written as |ψ> = cos(θ/2)exp(-iφ/2)|+> + sin(θ/2)exp(iφ/2)|->.

A system can be prepared in any state |ψ> by placing a Stern-Gerlach apparatus such that its axis is directed along the unit vector u and letting only the upward deflected particles pass.