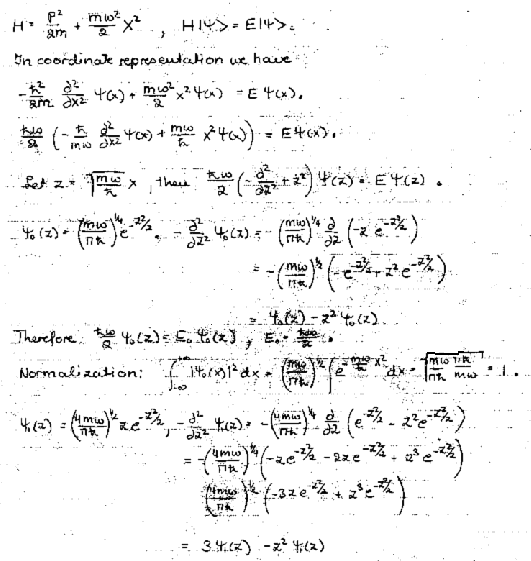
Show that all eigenstates of the Hamiltonian of the one-dimensional harmonic oscillator are not degenerate.

Solution:
We have already shown that the ground state of the one-dimensional harmonic oscillator is not degenerate.
All eigenstates of H are also eigenstates of N = a^†a.
Assume |Φ_n> is not degenerate.
H|Φ_n> = (n + ½)ħω|Φ_n>,  N|Φ_n> = n |Φ_n>.
Consider a vector |Φ_n+1> with  N|Φ_n+1> = (n + 1)|Φ_n+1>.
a|Φ_n+1> = c |Φ_n>,  a^†a|Φ_n+1> = ca^†|Φ_n>  = (n + 1)|Φ_n+1>.
|Φ_n+1> =  (c/(n + 1))a^†|Φ_n> for any |Φ_n+1> for which N|Φ_n+1> = (n + 1)|Φ_n+1>.
All vectors |Φ_n+1> are proportional to a unique vector a^†|Φ_n>.
The eigenvalue (n + 1) is therefore not degenerate.
We have shown:
|Φ₀> is not degenerate.
If |Φ_n> is not degenerate then |Φ_n=1> is not degenerate.
This implies that all eigenvalues are not degenerate.

A particle of mass m moves in one dimension in the potential energy function U(x) = ½mω²x².
(a)  Write down the Hamiltonian abd the time-independent Schroedinger equation.

(b)  Show that by appropriate choice of a dimension less coordinate z the Schroedinger equation can be written as
½ħω(-d²/dz² + z²)Ψ = EΨ.
Verify that normalized solutions to this equation are
Ψ₀ =  (mω/(πħ))^1/4exp(-½z²)    and    Ψ₁ =  (4mω/(πħ))^1/4 z exp(-½z²)
and find the corresponding eigenvalues E₀ and E₁ .

(c)  Suppose that at t = 0 the system was prepared in such a way that its wavefunction was Ψ =  (2mω/(πħ))^1/4exp(-z²).
What is the probability that a measurement of the energy at t = 0 would yield the value of E₀?
What is the probability that a measurement of the energy at t = 0 would yield the value of E₁?
(d)  Would the system remain in the state Ψ =  (2mω/(πħ))^1/4exp(-z²) for subsequent times?  Explain!

Solution:

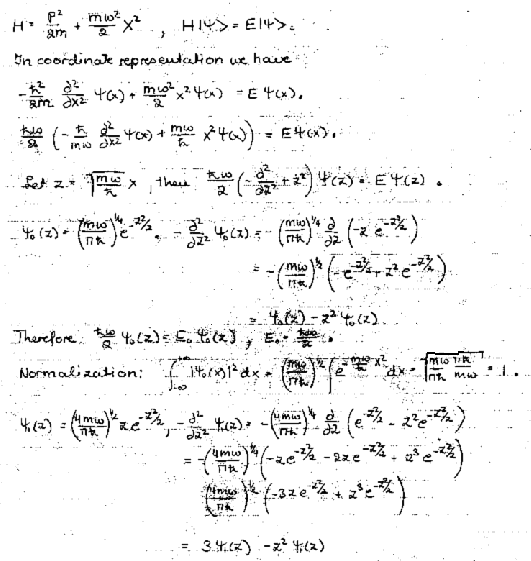
A system consists on N independent quantum mechanical harmonic oscillators of frequency f. The system is in thermal equilibrium with a reservoir at temperature T.
(a)  Calculate the average energy <E> for the system.
(b)  Find the heat capacity of the system when kT >> ħω.

Solution:

Consider a harmonic oscillator with Hamiltonian
H = ½P²/m + ½mω²X² = ħω(a^†a + ½).
Assume that at t = 0 the system is in the state |Ψ(0)> such that <Ψ(0)|a|Ψ(0)> = a₀.
(a) Show that <X>(t) behaves as a function of time as the coordinate x of a classical harmonic oscillator with amplitude x_M = (2ħ/(mω))^1/2|a₀|.
Such a classical harmonic oscillator has energy E = ½mω²x_M² = ħω|a₀|².
The expectation value of the energy of the quantum-mechanical oscillator is 
ħω<Ψ(0)|a^†a|Ψ(0)> + ½ħω.

(b) Assume that <a^†a>(0) = |a₀|²
Show that <a^†a>(0) = |a₀|² or <a>(0) = a₀ implies that a|Ψ(0)> = a₀|Ψ(0)>,
and that  a|Ψ(0)> = a₀|Ψ(0)> implies <a^†a>(o) = |a₀|² or <a>(0) = a₀.
The two conditions <a^†a>(0) = |a₀|² or <a>(0) = a₀ define what is called a quasi classical state.

(c) Let  |Ψ(0)> = ∑_nc_n|Φ_n>, H|Φ_n> = (n + ½)ħω|Φ_n>.
For a normalized |Ψ(0)> find the expansion coefficients c_n .

(d) Show that  ΔXΔP = ħ/2.

Sulution:

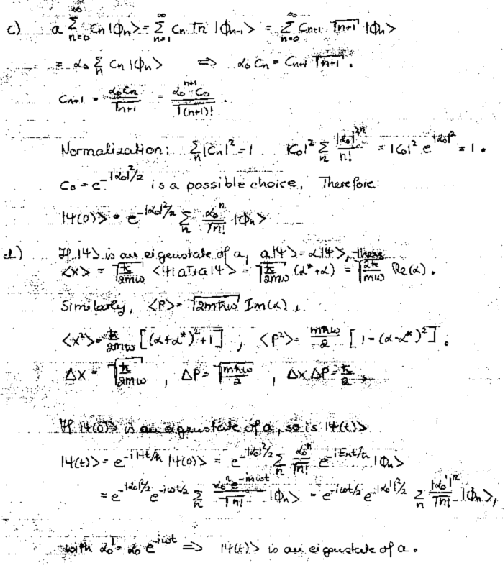
For the two-dimensional harmonic oscillator find the two lowest energy eigenstates and write down the corresponding wave functions.

Solution: