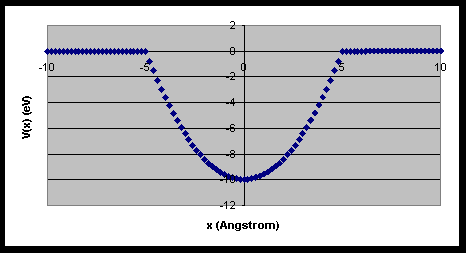
The program n4.txt is written in QuickBasic. It uses the WKB approximation to find the energies of the bound states in the one-dimensional potential shown below. The numerical integration uses Simpson's rule. For comparison, the program n3a.txt uses the same potential and integrates the time-independent Schroedinger equation numerically to find the energies of the bound states.
Explanation:The program n4.txt uses the WKB approximation to find the energies of the bound states of an electron in a potential V(x)=½kx2-10eV for |x|£ 5Å, and V(x)=0 for |x|>5Å, with k=(20eV)/(5Å)2.

The WKB approximation requires that
 .
.
For the chosen potential, the integral can be evaluated analytically. Let E'=E+10eV. Then
4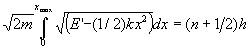 ,
,
xmax=2E'/k,
![]() ,
,
![]() .
.
These energies are the eigenenergies of the harmonic oscillator with V(x)=½kx2-10eV for all x. The WKB approximation for bound states does not distinguish between this potential and the harmonic oscillator potential V(x)=½kx2-10eV for all x when finding eigenenergies below 0eV.
The program n4.txt evaluates the integral  numerically using Simpson's rule.
numerically using Simpson's rule.
It assumes that V(x)=V0 fnv(x), where fnv(x)min=-1.
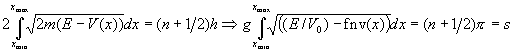
where
![]() .
.
The program first calculates the integral s for a very small value of E/V0. It then calculates the number of bound states it will look for by truncating s/p -0.5+1. The program guesses that the value of E/V0 for the lowest bound state is just slightly larger than -1. It changes the energy in small steps until s-0.5p is minimized. This yields the energy of the ground state, E0/V0. For the next excited state the program guesses E/V0 to lie just above E0/V0, i.e. just above the first value found. It changes the energy in small steps until s-(3/2)p is minimized, etc….
The chosen potential supports 4 bound states. The table below compares the results of the numerical integration with analytical results.
| WKB (analytical) | WKB (numerically) | |
| E0 | -8.766 | -8.765 |
| E1 | -6.296 | -6.295 |
| E2 | -3.828 | -3.824 |
| E3 | -1.358 | -1.354 |
The program n3a.txt finds the bound states for the same potential by numerically integrating the time-independent Schroedinger equation. For a description of the program click here. The potential in n3.txt was changed to yield n3a.txt. The energies found by this program are given below.
| E0 | -8.767 |
| E1 | -6.312 |
| E2 | -3.851 |
| E3 | -1.491 |
For the potential chosen here, the WKB approximation becomes less accurate as E increases, because it does not take into account that V(x)=0 for |x|>5Å. Near the edge of the well, the linear approximation that is used to derive the WKB approximation is valid only over a small range of x.