A numerical solution of the one- dimensional, time-independent Schroedinger equation.

Reference: S. E. Koonin, Computational Physics, Addison-Wesley Publishing Company Inc, (1986).

Numerov.xlsm is a macro-enabled Excel spreadsheet which demonstrates a method for solving the time-independent Schroedinger equation in one dimension.  This is a boundary value problem. We solve for the eigenvalues E of the Hamiltonian for which the wave function and its derivative are continuous and for which the wave function takes on given values at the boundaries of the integration volume.
Numerov.m is a MATLAB function implementing the same method.

Explanation:
We want to solve the eigenvalue equation
Hψ(x)  = Eψ(x),  
or  
(-ħ2/(2m))∂2ψ(x)/∂x2 + U(x)ψ(x)  = Eψ(x),
or
∂2ψ(x)/∂x2 - k2(x)ψ(x) = 0,
with k2(x) = (2m/ħ2)(E - U(x)).
We want to solve it in a finite region between x = -L and x = L.  We assume that in the middle of this region there exists a potential well of width a, with a/2 << L. 
Because we cannot extend our numerical solution to infinity, we assume that U(x) = ∞ for x < -L and x > L.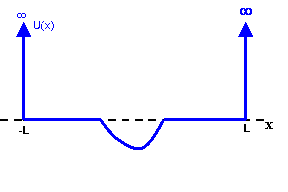


We want to find the energies for which the wave function ψ(x) and its derivative ∂ψ(x)/∂x are continuous and the boundary conditions ψ(0) = ψ(L) = 0 are satisfied.  These are the energies of the bound states of the system.

We start by expanding ψ(x) in a Taylor series expansion.
ψ(x + ∆x) = ψ(x) + ∆x*∂ψ(x)/∂x + [(∆x)2/2]*∂2ψ(x)/∂x2 + ... .
ψ(x - ∆x) = ψ(x) - ∆x*∂ψ(x)/∂x + [(∆x)2/2]*∂2ψ(x)/∂x2 - ... .
Combining the two equations above yields
[ψ(x + ∆x) + ψ(x - ∆x) - 2ψ(x)]/(∆x)2 = ∂2ψ(x)/∂x2,
or
[ψ(x + ∆x) + ψ(x - ∂x) - 2ψ(x)]/(∆x)2 = -k2(x)ψ(x).
ψ(x + ∆x) = (2 - (∆x)2k2(x))ψ(x) - ψ(x - ∆x).

For our numerical work, let {xn} denote points on a grid defined in the region from x = -L to x = L, n = 0, 1, …, N. 
Define ψn = ψ(xn),  kn = k(xn),  ∆x = xn+1 - xn.  Then
ψn+1 = (2 - (∆x)2kn2)ψn - ψn-1.
We have a recipe for finding ψn+1, given ψn and ψn-1.  Integrating the wave function using this algorithm, i.e. finding its value on the next grid point from its value at the previous two grid points, is called integrating using the Numerov method.

We can go to the next order in the expansion for higher numerical accuracy.  Numerov.xlsm goes to 2nd order in the expansion and numerov .m goes to 4th order.

Implementation:
To solve for the bound states of the system, we pick ψ0 = 0, ψ1 = c1, where c1 is some small number.  This number c1 determines the overall normalization of the wave function.  We now calculate ψ2, ψ3, etc. 

ψn+1 = (2 - (∆x)2kn2)ψn - ψn-1.

We start integrating in the classically forbidden region, where the magnitude of the wave function increases approximately exponentially.  As we reach the classically allowed region, the wave function becomes oscillatory at the classical turning point.  As we pass through the second turning point and enter again into the classically forbidden region, the integration becomes numerically unstable, because it can contain an admixture of the exponentially growing solution.  Integration into a classically forbidden region is likely to be inaccurate.  We therefore generate a second solution, picking ψN = 0, ψN-1 = c2, and calculating ψN-2, ψN-3, etc.

ψn-1 = (2 - (∆x)2kn2)ψn - ψn+1.

For both integrations we pick the same value for the energy E.  To determine whether this energy E is an eigenvalue, we compare the results of our integrations at a matching point xm in the classically allowed region.  The constant c2 is chosen so that both integrations yield the same value ψ(xm) at the matching point and we examine the slope ∂ψ(x)/∂x near xm.  The values of E for which the slope is continuous across the matching point are the energy eigenvalues, because for these values of E the wave function is a solution to the Schroedinger equation which satisfies all boundary conditions.  We search for the eigenvalues by picking different values for the energy E.

Procedure using manual matching:
Open the numerov.xlsm Excel spreadsheet  It can be used to solve the one-dimensional, time-independent Schroedinger equation for an electron trapped in various potential wells.  Sheet 1 contains the data and sheet 2 the user interface.

Examine sheet 1.

Switch to sheet 2.

Procedure using programmed matching:
We numerically integrate the wave function starting at both boundaries.  For both integrations we pick E = Umin + ∆E, i.e. we pick E just slightly larger than Umin.  To determine whether the energy is an eigenvalue, we compare the results of our integrations at a matching point xm in the classically allowed region.  We first re-normalize the wave functions ψ1 and ψ2 obtained from our two integrations such that ψ1m = ψ2m.  We then check if the derivatives of the two functions are equal at xm, i.e. if dψ1(x)/dx - dψ2(x)/dx = 0.
We use dψ2 = ψ2m - ψ2m-1,  dψ1 = ψ1m - ψ1m-1.
We already have made ψ2m = ψ1m.  We therefore only have to check if ψ2m-1= ψ1m-1. We define
f = [ψ2m-1- ψ1m-1]/ψmax.
If f ≠ 0 within a chosen limit of tolerance, then we repeat our integrations after incrementing E by ∆E.
If f ≠ 0 for two successive iterations, but f has changed sign, then the eigenvalue has been overshot.  We decrease the magnitude and change the sign of ∆E and start decrementing E.  We repeat until f = 0 within the chosen limit of tolerance.

How do we adjust ∆E to find the value of E for which f = 0?
Pick the initial energy E1.  Integrate and find f(E1).  If f(E1) ≠ 0 within a chosen limit, pick some initial ∆E to calculate E2 = E1 +  ∆E.  Integrate and find f(E2).  If f(E2) ≠ 0 within a chosen limit what value  ∆E should pick to find E3?  Hoe do you find the root of f(E)?

If f(Ei) ≠ 0 within a chosen limit, expand f(E) about Ei.
Then set f(Ei + ∆E) = f(Ei) + df/dE|Ei∆E = 0, where  ∆E = Ei+1 - Ei.
Ei+1 is the next better value for the root of f(E).
Ei+1 =  Ei - f(Ei)/(df/dE|Ei).
df/dE|Ei ≈ (f(Ei) - f(Ei-1))/(Ei - Ei-1).
Therefore
∆E = Ei+1 -  Ei = -f(Ei)(Ei - Ei-1)/(f(Ei) - f(Ei-1)).

The MATLAB function numerov.m implements programmed matching.