Atomic Spectra

Review: Simple spectra (one-electron atoms)

The eigenvalue equation for the Hamiltonian H0 of a particle with potential energy -Ze2/r is

.

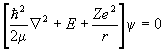Common eigenfunctions of H0, L2, and Lz are of the form ynlm(r)=Rnl(r)Ylm(q,f).

.

If E>0, then a solution exists for any value of E and l.

If E<0, then solutions exist only for discrete values of E, .

Definitions:

n=1 ground state ionization potential
n=2 resonance level resonance potential

For hydrogen EI=13.595eV, ER=10.196eV.

Definition of shells:

K L M N O
1s 2s 3s 4s 5s
  2p 3p 4p 5p
    3d 4d 5d
      4f 5f
        5g

Electric dipole transitions:

The probability per unit time of a spontaneous transition from a stationary state |a> to a stationary state |b>, accompanied by the emission of a photon of energy =Ea-Eb is

,

with xab=<a|x|b>.

The selection rules are Dl=±1, Dml=0, ±1, Dn is not restricted.

Series regularities:

.

R=109677.581cm-1 for hydrogen.

n'=1 n=2,3,4,… Lyman series
n'=2 n=3,4,5,… Balmer series
n'=3 n=4,5,6,… Paschen series
n'=4 n=5,6,7,… Bracket series
n'=5 n=6,7,8,… Pfund series

Notation for ionized atoms:

I=neutral, II=singly ionized, III=doubly ionized, … .
(Example: BeI, BeII, BeIII, … .)

Fine Structure:

H=H0+Hf.

.

First order energy shifts:

.

Dipole selection rules: Dj=0, ± 1,  Dmj=0, ± 1.

Spectra of multi-electron atoms

The Hamiltonian H0 for a multi-electron atom is

.

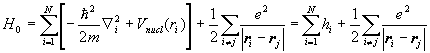H0y=Ey.

We often use the central field approximation.  We assume that each electron moves in a centrally symmetric field created by the nucleus and all the other electrons.  Let U(ri) denote the potential energy of electron i in the centrally symmetric field of all the other electrons.

.

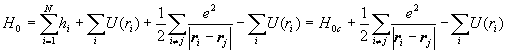H=H0c+H'.  We treat the non-central part of the potential as a perturbation of H0c.  This perturbation is referred to as electron-electron correlations.

To solve H0cy=Ey for the eigenfunctions and eigenvalues of H0c, we assume that y is of the form y=y1(r1)y2(r2)… .  Then the eigenvalue equation can be separated into equations of the form

.

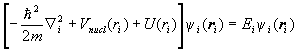For each electron we therefore have an equation of the form

.

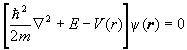The solutions are of the form y(r)=R(r)Ylm(q,f)c(x), where R(r) is a solution to the radial equation

.

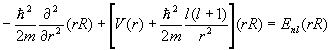We have N independent equations.  The central field approximation is therefore called an independent electron approximation.

The self-consistent field approximation

To calculate U(ri) due to the centrally symmetric field produced by all the other electrons, we must know the wave functions of all electrons.

Procedure:

Use a trial function of the form y=y1(r1)y2(r2)….
Assume some reasonable wave functions for the single electron wave functions, for example hydrogenic wave functions.
Calculate U(r).
Use U(r) in the eigenvalue equation for the Hamiltonian for each electron to calculate new wave functions for each electron using the variational method.
Use these new wave functions to calculate U(r).
Repeat the last two steps until self consistency is reached to a high order of accuracy.

The wave function y thus found is the optimum wavefunction that can result from a variational calculation with a trial function of the form y=y1(r1)y2(r2)….

Definitions:

State:
The state of an atom is the condition of motion of all the electrons.  To specify a state, one must list four quantum numbers for each electron, for example n,l,ml,ms, or n,l,j,mj.
Level:
A level is a collection of states having the same energy in the absence of an external electric and magnetic field.
Sublevel:
External fields split energy levels into several sublevels.
Configuration:
A configuration is an enumeration of the values of n and l for all electrons of an atom.
Equivalent orbitals:
Equivalent orbitals are orbitals with the same quantum numbers n and l.
Coupling scheme:
A coupling scheme is a recipe for adding angular momenta.

In the central field approximation 2(2l1+1)2(2l2+1)2(2l3+1) states, differing by the values of the quantum numbers ml and ms correspond to each configuration n1l1, n2l2, n3l3,… .  The non-central part of the electrostatic interaction between the electrons and the spin-orbit interaction lead to splitting of the level n1l1, n2l2, n3l3,… into a number of sublevels.

LS coupling

We assume that the non-central part of the electrostatic interaction is much bigger than the spin-orbit interaction.  (This is usually true for light multi-electron atoms.)  The electrostatic interaction leads to a splitting of the level corresponding to a given electron configuration into a number of sublevels characterized by different values of the total orbital angular momentum of the electrons, L, and the total spin, S.  The operator for the electrostatic interaction commutes with L=l1+l2+l2+… and S=s1+s2+s3+… .  (See Cohen-Tannoudji, page1000).  To each term LS belong (2L+1)(2S+1) states, differing by the values of ML and MS.  The spin-orbit interaction leads to a splitting of the term LS into a number of components corresponding to different values of the total angular momentum J.  But it does not completely remove the degeneracy.  Each J component is degenerate with a multiplicity of 2J+1.

.

In the LS coupling scheme, a term is designated by 2S+1LJ.  2S+1 is called the multiplicity of the term.

Which terms corresponding to a given configuration have the lowest energy?

Hund's Rule (established empirically)

The level with the largest multiplicity has the lowest energy.
For a given multiplicity, the level with the largest value of L has the lowest energy.
For less than half-filled shells:
The component with the smallest value of J has the lowest energy (normal order).
Examples of less than half-filled shells: np2, nd2
For more than half-filled shells:
The component with the largest value of J has the lowest energy (inverted order).
Examples of more than half-filled shells: np4, nd8
When the number of electrons is 2l+1, i.e. when the shell is half filled, there is no multiplet splitting.

Example:

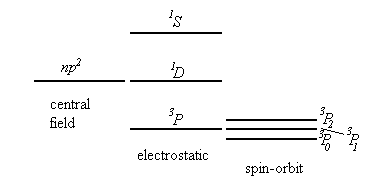
Image1330.gif (1999 bytes)

Finding the terms of a multi-electron configuration:

Non-equivalent electrons:
L=L1+L2, L1+L2-1, …, |L1-L2|
S=S1+S2, S1+S2-1, …, |S1-S2|
Addition is first carried out for two electrons, then the third is added, then the fourth, and so on.

Examples:

Configuration np, n'p
L=0,1,2, S=0,1
The terms 1S,1P, 1D, 3S, 3P, and 3D, are possible.
Configuration np, n'p, n''p

 

np, n'p [1S] n''p ----> 2P
np, n'p [1P] n''p ----> 2S, 2P, 2D
np, n'p [1D] n''p ----> 2P, 2D, 2F
np, n'p [3S] n''p ----> 2P, 4P
np, n'p [3P] n''p ----> 2S, 2P, 2D, 4S, 4P, 4D
np, n'p [3D] n''p ----> 2P, 2D, 2F, 4P, 4D, 4F

In brief form this is written as

2S P D F 4S P D F
  2 6 4 2   1 3 2 1

The number under the term symbol indicates the number of identical terms.

Equivalent electrons:

Among the values of L and S obtained from the general rules for addition of angular momenta are those which correspond to states forbidden by the Pauli principle.

Examples:

Configuration np2

For each electron the following values are possible:
ml=1,0,-1,  ms=1/2,-1/2
Combining the different values of ml and ms, we obtain the following possible states:

ml=1 ms=1/2 (1+)
ml=0 ms=1/2 (0+)
ml=-1 ms=1/2 (-1+)
ml=1 ms=-1/2 (1-)
ml=0 ms=-1/2 (0-)
ml=-1 ms=-1/2 (-1-)

In each of these states there cannot be more than one electron.

The following states with non-negative values of ML and Ms are possible.

State ML Ms
(1+)(0+) 1 1
(1+)(-1+) 0 1
(1+)(1-) 2 0
(1+)(0-) 1 0
(1+)(-1-) 0 0
(0+)(1-) 1 0
(0+)(0-) 0 0
(-1+)(1-) 0 0

State with negative values of ML and Ms need not be written out.

The presence of the ML=2, Ms=0 term shows that a 1D term is among the possible terms. To this term we must further assign states with ML=1, Ms=0 and ML=0, Ms=0.
Among the states left is a state with ML=1, MS=1. This and and states with  ML=1, MS=0, and ML=0, MS=1, and ML=0, MS=0 yield the 3P term.
The only remaining state has ML=0, MS=0. It corresponds to the 1S term.

Thus only three terms are possible, 1D, 3P, and 1S for the configuration np2.

The possible terms for the configuration np3 are 4S, 2P, and 2D.
The possible terms for the configuration np4 are 1D, 3P, and 1S, the same terms as for the configuration np2.

The statistical weight is the total number of terms pertaining to a given configuration.

For a configuration with no equivalent electrons the statistical weight is

.

For the configuration ln, the statistical weight is determined by the number of possible combinations which can be formed from the quantum numbers ml, ms taking into account the Pauli principle. Let N0=2(2l+1).  The statistical weight of ln is

.

jj coupling

We assume that the spin-orbit interaction considerably exceeds the non-central part of the electrostatic interaction. (This is usually true for heavy multi-electron atoms.)  Then the energy depends primarily on how the orbital angular momentum li and the spin angular momentum si of each electron sum up into the total angular momentum ji of each electron. j1=l1+s1, j2=l2+s2, … .  The electrostatic interaction now leads to a splitting, depending on how the vectors ji sum up into the total angular momentum J.  In the jj coupling scheme the state of each electron is described by four quantum numbers, n, l, j, mj, where j=l ±1/2.

Notation for each electron:

1s1/2, 2s1/2, 2p1/2, 2p3/2, …

If we neglect the electrostatic energy completely, then the energy of each electron is determined by the quantum numbers nlj.  The level corresponding to each j is 2j+1 fold degenerate.

Example:

Configuration np, n'p

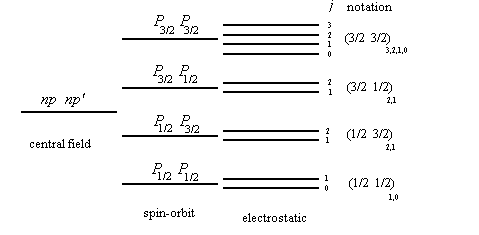
Image1333.gif (2789 bytes)

Configuration np2
    possible terms
np1/2 , np1/2 m1=1/2, m2=-1/2 (1/2,1/2)0
np1/2 , np3/2 m1= ±1/2, m2= ±1/2, ±3/2 (1/2,3/2)2,1
np3/2 , np3/2 m1=3/2, m2=1/2
m1=3/2, m2=-1/2
m1=3/2, m2=-3/2
m1=1/2, m2=-1/2		 (3/2,3/2)2,0