The Dirac equation for a spin ½ particle is of the form

For a free particle

with a_x²=a_y²=a_z²=b²=1 and all four quantities a_x, a_y, a_z, and b anti-commuting in pairs.

For example a_xa_y+a_ya_x=0.

Since a and b anti-commute, they cannot be numbers.  For a spin ½ particle a_x, a_y, a_z, and b are represented by 4´4 matrices.

In compact notation

where each entry is a 2´2 matrix.

Given a and b as 4´4 matrices, y(r,t) must be a matrix with 4 rows and 1 column.

is equivalent to 4 coupled first order, linear, homogeneous, partial differential equations for the 4 y’s.  Plane wave solutions of the form y_j(r,t)=u_jexp(i(k ×r-wt)), j=1,2,3,4 can be found, where the u_j are numbers.  These are eigenfunctions of the energy operator and momentum operator with eigenvalues  respectively.

Substituting these plane wave solutions into yields a set of algebraic equations for the u_j, where are now numbers, not operators.

.

.

.

.

These equations are homogeneous in the u_j and have a solution only if the determinant of the coefficients is zero.  This determinant equals Explicit solutions can be obtained for any p by choosing a sign for the energy, say  Then there are two linearly independent solutions, which are conveniently written as

If we choose the negative square root, then we obtain two different solutions, which are written as

Each of these 4 solutions can be normalized in the sense that yy*=1 by dividing it by

In the non relativistic limit E₊ is close to mc² and much larger than c|p| and for the positive energy solutions u₃ and u₄ are approximately a factor v/c smaller than u₁ or u₂.

The Dirac Hamiltonian for a spin ½ particle in the presence of an electromagnetic field is

and the time independent Dirac equation may be written as

in SI units.  For a particle with charge q in a spherically symmetric scalar potential we have

The Dirac equation for an electron in the field of a proton

Assume   i.e. neglect the spin of the proton.  (q_e=1.6×10^-19C)

Assume 

Then the orbital angular momentum L is not a constant of motion.

In the Heisenberg picture we have

Let us define the operator s’, which is represented by the matrix 

The operator s’ is not a constant of motion.  We have

But we can see that the operator  is a constant of motion. It commutes with H_D.  This operator is interpreted as the total angular momentum operator.  The operator  is referred to as the spin angular momentum operator.

Let  in compact notation, both y₁ and y₂ having two components.  We may then write the eigenvalue equation for H_D ,

as

This yields

and

We can use the second equation to obtain

and substitute this expression for y₂ into the first equation. We the obtain

or

In the non relativistic limit

In the above equation p is an operator, Therefore pf is an operator, which may be written as   We may write

using the general result

[We can apply this equation to the operators since s commutes with p and the gradient of f, and the order of p and the gradient of f is not changed.]

Therefore

For a spherically symmetric potential  V=-q_ef   we have 

In the non relativistic limit we also have and Therefore

where 

The first and third term give the non relativistic Schroedinger equation, the second term has the form of the classical relativistic correction, the last term is the spin-orbit energy, which appears as an automatic consequence of the Dirac equation.  The fourth term is a similar relativistic correction to the potential energy, which does not have a classical analog.  It is called the Darwin term.
The ratio of < all the correction terms > to < > is on the order of v²/c².

[Note that y₁ is the two component spinor as used in the non relativistic description of a spin ½ particle.]

If we do not neglect the spin and the magnetic moment of the proton, we cannot set A(r,t)=0.  We now have to replace p by (p-qA), where q=-q_e.  We obtain the equation

We assume that < q_eA > << <p> and only keep terms to the lowest order in q_eA.  We also neglect terms that contain Then only one new term is added to our equation for E’ derived when A(r,t)=0.  We find the new term by evaluating

We have in general Therefore

[ is an operator. When it operates on a wavefunction y we have

]

The new term therefore is

and

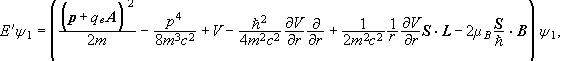
The first term contains the spin-orbit interaction energy of the proton and the last term the spin-spin interaction energy.  Both terms are hyperfine structure terms.

The hyperfine structure Hamiltonian (neglecting terms in (qA)²) is

It may be rewritten as

since A is the vector potential due to the magnetic moment of the proton and (See Cohen-Tannoudji, Complement A_XII.)

The fine structure Hamiltonian is

H = H₀ + W_f + W_hf.

The ratio is on the order of