An electron approaching a stationary atomic target with a given velocity can elastically scatter off the target.  We will calculate the differential cross section for the elastic scattering of electrons from atomic hydrogen. The partial wave method will be used to solve the scattering problem.  For different values of the orbital angular momentum we will integrate the radial part of the time independent Schroedinger equation numerically using the Numerov method.  This will yield the phase shifts which are needed to calculate the cross sections.

Method of solution

The differential scattering cross section for electrons incident on a spherically symmetric finite range potential using the method of partial waves is given by

   (1)

This expression can be rewritten in terms of only real numbers as

,    (2)

where

  (3)

and

.   (4)

In equations (3) and (4) the letter l denotes an index that runs from zero to infinity.  For large l we expect d_l to be zero.  The square root of the electron energy is proportional to k. The P_l(cosq) denote the Legendre polynomials.  These are well known functions which can be calculated from a recursion formula.  The only unknowns in equations (3) and (4) are the d_l. They are called the phase shifts for the different partial waves. There are infinitely many of them, one for each l, from l=0 to l=¥.  But we do not have to calculate an infinite number of phase shifts.  The terms in the above sums for large l become very small, because the phase shifts d_l for large l are much smaller than one and sind_l is approximately zero. If l becomes greater then some number l_max, then the terms in the sum become so small that they can be neglected.  One of the challenges of computing s(q) is to decide how many terms to include, i.e. to decide when a term is small enough to be neglected.

To calculate the d_l we have to solve the Schroedinger equation numerically.  The radial part of the wavefunction of the partial wave with index l is u_l(r)/r. Here r denotes the distance from the scattering center.  The function u_l(r) is a solution of

   (5)

For large r the solution of this differential equation has the form

.   (6)

Here j_l and n_l are the regular and irregular spherical Bessel functions of order l.  Again, these are well known functions which can be calculated from a recursion formula.

To find d_l we integrate equation (5) numerically using the Numerov method.  (See Program 3, QM1.)  To do this integration we need to know the potential V(r), which describes the forces between the scattering electron and the atom. We need an accurate potential.  The potential is a sum of two terms, one term, -e²/r, due to the proton nucleus and one term due to the electron of the hydrogen atom.  We assume that the electronic charge density is -e|y(r)|², where y(r) is the normalized hydrogen atom ground state wavefunction.  We can then calculate using Gauss’ law and find V(r) from Summing up the two terms we obtain   The potential will be of finite range, i.e. for distances greater than some distance r_max away from the center of the atom it will be effectively zero.

For the integration we divide the distance from the scattering center to some distance r_ext, which is greater than r_max, into a large number of small segments of length dr.  For each segment we can calculate u_l(r) if we know u_l(r) in the preceding two segments.  Let n denote the nth segment. If we write

  ,   (7)

then

(8)

Setting u_l(0)=0 and u_l(1) to some small number which determines A in equation (6), we can calculate u_l(2).  From u_l(1) and u_l(2) we calculate u_l(3) and in the same fashion we proceed to calculate u_l(n) for all n up to the n which corresponds to r_ext.  Between r_max and r_ext we assume that u_l(r) is of the form given in equation (6).  Then we can find d_l from

with    (9)

One of the challenges of the numerical calculation is to choose r_max correctly.  If we choose it too small then the calculation will be inaccurate.  If we choose it to large we are likely to introduce numerical errors into the calculation.  Another challenge is to choose the right step size for the numerical integration of the Schroedinger equation.  The potential V(r) changes rapidly near the center of the atom.  We need a very small step size to pick up these changes.  But a calculation with a very small step size takes a very long time.  Furthermore, farther away from the center of the atom the potential changes very slowly and a bigger step size is warranted.

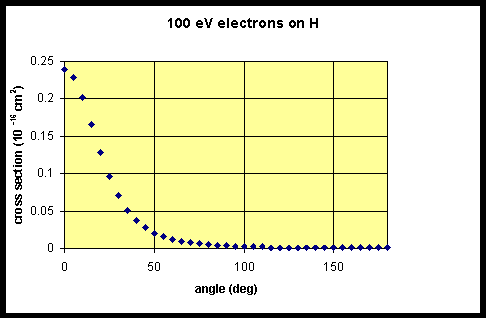
The calculated differential scattering cross section for 100eV electrons scattering off hydrogen is shown below.  Note: The program is slow.