Force and torque on moving charges, current carrying wires, and dipoles
Moving charges
Problem:
An electron gun T emits electrons accelerated by a potential difference U in
a vacuum in the direction of the line a as shown in the figure below. The
target M is placed at a distance d from the electron gun in such a way that the
line segment connecting the points T and M and the line a subtend the angle α as
shown in figure.
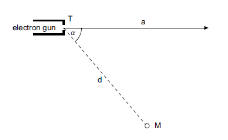
Find the magnitude B of the uniform magnetic field
(a) perpendicular to the plane determined by the line a and the point M
(b) parallel to the segment TM
in order for the electrons to hit the target M. Find first the general
solution and then substitute the following values:
U = 1000 V, α = 60o, d = 5.0 cm, B < 0.030 T.Solution:
- Concepts:
The Lorentz Force
- Reasoning:
A charged particle moving in a magnetic field is acted on by a force
F = qv × B.
- Details of the calculation:
(a) If a uniform
magnetic field is perpendicular to the initial direction of motion of an
electron beam, the electrons will be deflected by a force that is always
perpendicular to their velocity and to the magnetic field.
Consequently, the beam will be deflected into a circular trajectory. The
origin of the centripetal force is the Lorentz force, so Bqev
= mev2/r.
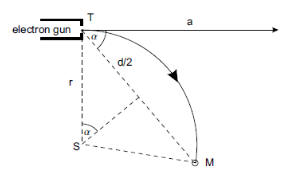
Geometry yields r = d/(2 sinα)
The velocity of electrons can be determined from ½mev2
= qeU.
Substituting yields B = me(2qeU/me)½(2sin
α/(qed)) = 2(2meU/qe)½sin α/d.
Substituting the given values we have B = 3.7*10-3 T.
(b) If a uniform magnetic field is neither perpendicular nor parallel to the
initial direction of motion of an electron beam, the electrons will be deflected
into a helical trajectory. The motion of electrons will be composed of uniform
circular motion in the plane perpendicular to the magnetic field and of a
uniform rectilinear motion in the direction of the magnetic field. The component
v1 of the initial velocity
v which is perpendicular to
the magnetic field will rotate uniformly around the line parallel to the
magnetic field. The component v2 parallel to the
magnetic field will remain constant.

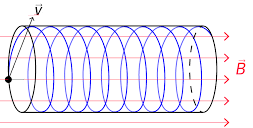
Magnitudes of the components of the velocity can be expressed as
v1 = v sinα, v2 = v cosα.
Denoting by N the number of screws of the helix we can write for the time of
motion of the electron t = d/v2 = d/(v cosα) = 2πrN/v1 =
2πrN/(v sinα)
Hence we can calculate the radius of the circular trajectory r = d sinα/(2πN
cosα).
The Lorentz force must be equated to the centripetal force.
Bqev sinα = mev2 sin2α/r = 2πN mev2
sinα cosα)/d.
B = 2πN mev cosα)/(d qe).
The magnitude of velocity v again satisfies v = (2qeU/me)½,
so
B = (2πN cosα)/d)(2meU/qe)½.
Numerically we get B = N*6.7*10-3 T.
If B < 0.030 T, then we
have four possibilities, N = 1, 2, 3, 4. B1 = 6.7*10-3
T. B2 = 13.4*10-3 T. B3 = 20.1*10-3
T. B4 = 26.8*10-3 T.
Problem:
Find the magnetic force on
charge q moving with velocity v due to another charge q' moving with
velocity v' when the positions of the charges are
r and
r' ,
respectively. (This is a non-relativistic problem.)
Solution:
- Concepts
The magnetic force
- Reasoning:
The magnetic force on a point
charge q moving with velocity v is
F = q(v
× B).
Treat the moving charge as a current element.
The magnetic field produced by a current element Idl located at
r'
is
B(r) = (μ0/4π) Idl
× (r-r')/|r-r'|3.
- Details of the calculation:
For charge q' moving at a velocity v' we have Idl = q'v'.
We therefore have
F = (μ0/4π) qq'(v
× v' × (r-r')/|r-r'|3).
Problem:
A particle
with mass M and charge q > 0 moves in a uniform magnetic field
B and also in the
field of another charge Q < 0 located at the origin. At t = 0 the particle is
at x = z = 0, y = a, and its velocity is v0i. For what
B will the
trajectory of the particle be a circle of radius a centered at the origin?
Solution:
- Concepts:
The Lorentz force
- Reasoning:
The Lorentz force, F = q(E + v
x B)
provides the centripetal force required for a circular orbit.
- Details of the calculation:
Consider the geometry shown in the figure below. Let
B
= Bk.
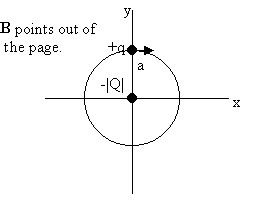
For a circular
orbit of radius a we need
Mv02/a = keq|Q|/a2 + qv0B,
B = Mv0/qa - ke|Q|/v0a2.
If B is negative, then B points into the page
Problem:
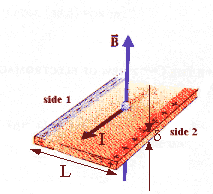
A current I is flowing in the metal strip of width L and thickness
d shown above. The
metal contains ne free electrons per unit volume. A
magnetic field B penetrates the strip as shown. In terms of I, B, ne,
and L, find the potential difference between side 1 and side 2.
Solution:
- Concepts:
The Hall effect
- Reasoning:
The current in the metal strip shown above is flowing because a power supply
establishes an electric field E in the strip. The conduction
electrons move with an average drift velocity vd opposite to
the direction of E. In the uniform field B the
magnetic force on each electron is F = -ev x B.
It causes the electrons to drift towards side 1 of the strip, leaving excess
positive charge on side 2. These separated charges produce the electric
field EH. The electrons will stop drifting sideways,
when the electric force -eEH cancels the magnetic force -ev
x B.
The resulting potential difference across the strip is∆V = V2 - V2 = EHL = vdBL.
This is known as the Hall potential.
If positive charges were moving in the strip, they would drift towards side 1
and the sign of the Hall potential would change.
- Details of the calculation:
The magnitude of the current I moving through a wire is given byI = |ρ-|<v->A =
neevdA,
where ne is the number of free electrons per unit volume.
The current I equals the number of electrons that pass any point along the wire
per second times the unit of charge e. <v-> = vd is the drift speed of
the electrons. It is their average speed, as they move along the wire.
We have vd = I/neeA = I/neeLδ.
∆V = IB/neeδ.
Problem:
Consider an idealized ion beam of radius R and length much longer than R.
Show that an individual ion at the periphery of this beam is subject to
the net outward force F = (1/(4πε0))(2Iq/Rv)(1 - v2/c2) where I
is the beam current, q is the charge of each ion, and v is the
velocity of the ions. Assume that the charge and current densities have
cylindrical symmetry.
Solution:
- Concepts:
Ampere's law, Gauss' law, the Lorentz force
- Reasoning:
Because of the cylindrical symmetry we can find the electric and magnetic
fields from Gauss' law and Ampere's law, respectively. We can then find
the force F = q(E + v x B)
on an individual particle with charge q.
- Details of the calculation:
In SI units:
Gauss' law: At r = R we have 2πRE
= I/(vε0), E = I/(2πε0Rv).
[The charge per unit length in the beam is λ =
I/v.]
Ampere's law: At r = R we have 2πRB
= μ0I = I/(ε0c2),
B = I/(2πRε0c2).
If the current flows in the z-direction then E points into the
r direction and B points into the
Φ direction.
The force on an ion of charge q moving with velocity vk at
r = R is F = q(E +
v x B)
F = qI/(2πε0Rv) - qIv/(2πRε0c2)
= qI/(2πε0Rv)(1 - v2/c2)
= (1/(4πε0))(2Iq/Rv)(1 - v2/c2).
The force points in the r direction and has magnitude F = (1/(4πε0))(2Iq/Rv)(1 - v2/c2).
Problem:
Two particles have equal mass m
and opposite electric charge +q and -q, and are embedded in a uniform magnetic
field B that is perpendicular to the line connecting the charges. The particles
are initially held at rest, then are released simultaneously.
(a) Find the force on each particle.
(b) Find the minimum initial separation L that will not result in a collision
after release. You can neglect gravitational effects.
Solution:
- Concepts:
F = q(E +
v x
B)
- Reasoning:
The particles interact via the electrostatic force, and if they are
moving they are acted on by the magnetic force.
The force on each particle is given by F = q(E +
v
x B).
- Details of the calculation:
(a) Place the positive charge on the x-axis at x = L/2 and the negative
charge on the x-axis at x = -L/2. Let the magnetic field point in the
z-direction.
The vector force acting on the negative charge is the mirror image of the
vector force acting on the positive charge when reflected through the x = 0
plane, and the trajectory of the negative charge is the mirror image of the
trajectory of the positive charge.
Force on the positive charge: Fx = -kq2/(4x2)
+ qvyB, Fy = -qvxB.
(b) The minimum initial separation L that allows the particles
not to collide will result in the particles traveling parallel to each other
in the y-direction with constant speed. The electric and magnetic forces
acting on each particle then add to zero. Let us use SI units. Let k =
1/(4πε0).
Force on the positive charge: Fx = -kq2/(4x2)
+ qvyB, Fy = -qvxB.
This yields ax = -kq2/(4mx2) + qvyB/m,
ay = -qvxB/m.
dvy/dt = -(qB/m)dx/dt.
For a particle starting at rest at x0 = L/2 we have ∫0vydv'y
= -(qB/m) ∫x0x
dx'.
vy = (qB/m)(x0 - x).
Therefore ax = (qB/m)2(x0 - x) - kq2/(4mx2).
For a particle starting at rest at x0 = L/2, energy conservation
yields
½m(vx2 + vy2) = ½kq2(1/(2x)
- 1/(2x0)).
vx2 + vy2 = [kq2/(2m)](1/x
- 1/x0)).
vx2 + (qB/m)2(x0 - x)2
= [kq2/(2m)](1/x - 1/x0)).
For the particle not to collide at the minimum distance we need ax
= vx = 0 for some x > 0.
For ax = 0 we need (qB/m)2(x0 - x) = kq2/(4mx2).
(i)
For vx = 0 we need (qB/m)2(x0 - x)2
= [kq2/(2m)](1/x - 1/x0))
or (qB/m)2(x0 - x) = kq2/(2mxx0). (ii)
Combining equations (i) and (ii) yields kq2/(4mx2) =
kq2/(2mxx0), or x0 = 2x.
Inserting x0 = 2x into either equation (i) or (ii) yields x =
(km/(4B2))(1/3).
Therefore x0 = 2(km/(4B2))(1/3), L = 4(km/(4B2))(1/3).
The minimum initial
separation L that allows the particles not to
collide is
L = 4(km/(4B2))(1/3).
Wires
Problem:
Two long
straight parallel wires carrying the same current
I and separated by a
distance r exert a force of magnitude F on each other. The current is
increased to 4I and the separation is reduced to
r/6 . What
will be the force between two wires?
Solution:
- Concepts:
Ampere's law, the magnetic force
- Reasoning:
We are asked to find the force between parallel current carrying wires.
- Details of the calculation:
From Ampere's law and F = Il × B we find the magnitude force (per unit length) between two parallel
current-carrying wires separated by a distance r.
F = μ0I1I2/(2πr). Here I1 = I2
= I, so F = μ0I2/(2πr).
If the current increases to 4I and the separation is reduced to r/6, then
Fnew = F = μ0 16 2/(2πr/6) = 96 μ0I2/(2πr)
= 96 F.
Problem:
A wire having a mass per unit length of 0.5 g/cm carries a 2 A current
horizontally to the south. What are the direction and magnitude of the minimum
magnetic field needed to lift this wire vertically upward?
Solution:
- Concepts:
The magnetostatic force on a wire, F = ∫V I dlxB(r)
- Reasoning:
We are to determine the minimum magnetic field needed to produce a force
F = -mg.
- Details of the calculation:
Orient your coordinate system so that the x-axis points towards the south
and the z-axis points upward. We want the direction of the magnetic force
F= IL x B on the wire segment to be
upward and the magnitude to be equal to mg. To get the maximum F for the
minimum B, B hat to point into the y-direction. Then F = ILB.
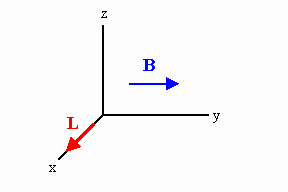
To lift the wire we need
B = mg/(IL) = ρLg/(IL)
= ρg/I = (0.05 kg/m)(9.8 m/s2)/(2 A) =
0.245 T.
We need B = 0.245 Tj.
B points eastward.
Similar problems
Problem:
A circuit contains two long straight wires laid out on a horizontal surface and
an ideal source of emf ε, all fixed in place. A straight wire of length l is
symmetrically placed on the wires as shown and initially held in place. The
resistance of a unit length of all wires is λ. The mass of the wire of length l
is m. The angle θ is given. The circuit is placed in a uniform magnetic field
B directed into the page and the wire of length l is released. Neglecting
friction and the induced emf, find the maximum speed of the wire after it is
released.
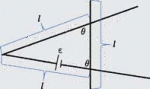
Solution:
- Concepts:
The magnetic force on a current-carrying wire
- Reasoning:
Choose a coordinate system with the x-axis pointing towards the right and the
origin where the long straight wires come together. Then the horizontal
position of the wire of length l at t = 0 is x0 = l sinθ.
When a current flows through the wire of length l, a force pointing to the right
will act on it. If it is free to move, it will accelerate towards the right.
It will lose contact with the rails when its horizontal position is x1
= (l/2)tanθ and stop accelerating.
- Details of the calculation:
Let 0 < θ < 90o.
The resistance of the circuit as a function of the horizontal position of the
wire x is
R = λ(2/cosθ
+ 2/sinθ)x
= C1x. C1 = λ(2/cosθ
+ 2/sinθ)
= constant.
The current flowing is I = ε/R = C2/x. C2 = ε/C1
= constant.
The magnitude of the force on the wire is I(2x cosθ)B = C22 cosθ B =
constant.
The acceleration of the wire is constant, a = C3 = (εB/λ)cos2θsinθ/(cosθ
+ sinθ).
Kinematics: vmax2 = 2ax1 = (lεB/λ)cosθsin2θ/(cosθ
+ sinθ).
Problem:
An infinitely long solenoid is wound with one layer of very fine wire.
The solenoid has a radius r meters, has n turns per meter of length, and carries
a current I.
(a) What is the magnetic field inside the solenoid?
(b) What is the magnitude of force on a short length dl of wire in a turn, and what is its direction?
(c)
What is the tension in the wire?
Solution:
- Concepts:
Ampere's law, the Lorentz force
- Reasoning:
The problem has enough symmetry to let us calculate B from Ampere's law
alone.
If the axis of the coil is the z-axis and the currents flow in the φ-direction,
then B = Bzk,
Bz = μ0In inside the coil and
B = 0 outside the coil. The current
in the wires may be treated as a surface current with surface current
density k. The field very close to a section of surface with current density
k
may be decomposed into the field B1 produced by the
section itself and the field B2 produced by all other
surrounding sections. The force per unit length on each wire can be
found by from F= IL x
B2.
- Details of the calculation:
(a) The magnetic field inside the solenoid is
B = Bzk,
Bz = μ0In.
(b) Consider a closed loop of length L enclosing N wires of the coil
as shown.
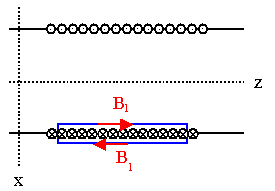
The current flowing through the loop is NI, and very near the wires this
current NI produces the same B1 field as a surface
current with density k = NI/L flowing in the same direction in a flat
surface. Ampere's law yields B1 = μ0NI/2L
= μ0In/2 pointing into the z direction
on the inside and into the -z direction on the outside of the coil. So
the field near the N wires that is produced by currents not flowing in the vicinity
of the loop is B2 = μ0In/2
k. From F = ILxB2 we now find
the force per unit length F/L = μ0I2n/2
pointing in the positive r direction.
Alternate approach based on energy considerations:
The energy stored in the magnetic field in the coil in a section of unit
length is
U = (1/(2μ0))B2A = (1/(2μ0))(μ0In)2A
= I2n2μ0πR2/2.
If we change the radius of the coil while keeping the current constant then
the stored energy increases at a rate
dU/dt = I2n2μ0πRdR/dt.
The rate at which the battery does work to maintain constant current in the
filementary circuit is
I*emf = I d(In2μ0πR2)/dt
= 2I2n2μ0πRdR/dt
= 2dU/dt. (emf is equal to the rate of change of the
flux through the coil.)
If dR is positive, then the battery does positive work.
dU = Wbat + Wext = 2dU + Wext.
Wext = -dU
The rate at which work is done by the circuit per unit length of coil
therefore is
dW/dt = -dWext/dt = dU/dt = I2n2μ0πRdR/dt.
dW/dt =
2πRfr∙v = 2πRfrdR/dt.
Therefore 2πRfr = I2n2μ0πR.
The force per unit length along the circumference fr points radially outward.
The force
per unit length along the circumference on a single wire is fr/n = Fr/(n2πR) = I2nμ0/2.
(c) Consider a wire loop acted on by a radial force. The
magnitude of force per unit length is constant. If the loop is cut
into two equal pieces, then the total force pulling the pieces apart is
Fz = 2*(I2nμ0/2)∫0π/2cosθ
rdθ = I2nμ0r.
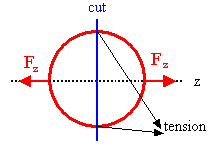
For the two pieces of the loop to not accelerate away from each
other we need 2T = Fz, where T is the tension in the wire.
Therefore T = I2nμ0r/2.
Dipoles
Problem:
A rectangular loop consists of N closely wrapped turns and has dimensions a =
0.4 m and b = 0.3 m. The loop is hinged along the y-axis and its plane makes an
angle of 30o with the x-axis.
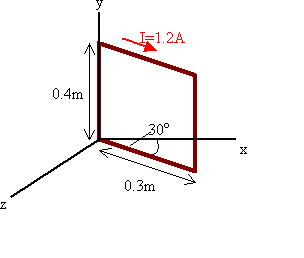
What is the magnitude of the torque exerted on the loop by a uniform magnetic
field B = 0.8 T directed along the x-axis when the current I is 1.2 A in the
direction shown?
What is the expected direction of rotation of the loop?
Solution:
Problem:
Assume a system has a magnetic dipole moment m because it has orbital
angular momentum L. If the dipole is at an angle θ to a
uniform magnetic field B, find the precession frequency Ω
in terms of L/m.
Solution:
- Concepts:
Torque on a magnetic dipole in a magnetic field
- Reasoning:
τ =
m
× B = (m/L) L
× B = -(m/L) B
× L
τ = dL/dt =
Ω
× L
- Details of the calculation:
Ω
= -mB/L
Problem:
A sphere with magnetic dipole
moment m and moment of inertia I about an axis through its center is placed in a
uniform magnetic field B. Find the period of small oscillations of the dipole.
Solution:
- Concepts:
Torque on a magnetic dipole in a magnetic field
- Reasoning:
τ = μ ×
B = Iα
We will have small oscillations if d2θ/dt2 =
-constant*θ
- Details of the calculation:
Let B point in the z-direction and
μ make an angle θ with the
z-axis.
Then τ = μBsinθ = -I d2θ/dt2
For small oscillations: Id2θ/dt2 = -μBθ, θ = θ0sin(ωt
+ ϕ), ω2 = μB/I,
Therefore the period T = 2π(I/(μB))½.
Problem:
A loop of wire is shaped like a regular plane polygon of 2n sides.
The distance between parallel sides is 2a.
The loop carries a current I.
The loop is placed in a uniform magnetic field B.
Find the magnitude torque on the loop.
How does it depend on the direction of B?
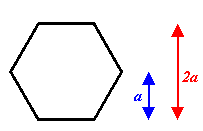
Solution:
- Concepts:
The magnetic moment of a current loop, the torque on a
current loop in a magnetic field
- Reasoning:
We are asked to find the magnitude of the torque on a current loop.
- Details of the calculation:
The torque on a current is τ = μ
x B. The magnetic
moment is μ = IAn. (Only the area of the loop, not the shape,
matters.) The direction n of
μ is given by the right hand
rule. For the loop placed as shown and the current flowing
counterclockwise, μ points out of the page. The area of the loop is A
= 2na2tan(π/(2n)).
τ = IAsinθ = I2na2tan(π/(2n))sinθ, where θ is the angle
between the directions of μ and B.
Problem:
A metal wire of length L is formed into a loop, either square or circular.
A current I flows through the loop and it is placed in a uniform magnetic
field. Which loop shape results in a larger torque? Why?
Solution:
The magnetic moment of a current loop, the torque on a current loop in a
magnetic field
The torque on a current is τ = μ
x B. The magnetic moment
is μ = IAn. (Only the area of the loop, not the shape, matters.)
The direction n of μ is given by the right hand rule. The
magnitude of the torque is τ = IAsinθ, where θ is the angle between the
directions of μ and B.
For a given length of wire L, the area of the circular loop is L2/(4π)
and the area of the square loop is L2/16. For a given θ, the torque
on the circular loop is larger.
Solution:
- Concepts:
The magnetic moment of a current loop, the torque on a current loop in a
magnetic field
- Reasoning:
The torque on a current is τ = μ
x B. The magnetic moment
is μ = IAn. (Only the area of the loop, not the shape, matters.)
The direction n of μ is given by the right hand rule. The
magnitude of the torque is τ = IAsinθ, where θ is the angle between the
directions of μ and B.
- Details of the calculation:
For a given length of wire L, the area of the circular loop is L2/(4π)
and the area of the square loop is L2/16. For a given θ, the torque
on the circular loop is larger.
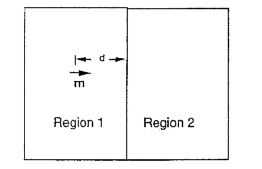
A point magnetic dipole
m in vacuum (region 1 in the diagram below) is
pointing toward (and is normal to) the plane surface of a material with
permeability μ (region 2). The distance between
the dipole and the surface is d.
(a) Use the method of images to find the magnetic field
B in both
regions, as follows: Place an image dipole m' = αm a distance d into medium 2 and take the field
B1
in region 1 to be due to dipoles m and
m'
in a medium with
μ0. Take the field B2 in region 2 to be due to a single dipole
m" =
βm at the location of
the real dipole m in a medium with μ. Solve the boundary value problem at the
interface to evaluate B1 and
B2.
(b) Describe physically how each of the image dipoles
m' and
m"
arise and the role they play in determining the fields and the forces on the
real dipole and the material of medium 2.
(c) Evaluate the force acting on the dipole m.