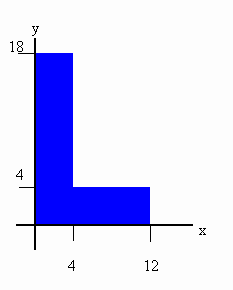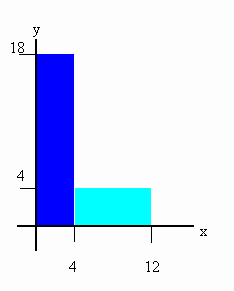Moment of inertia and CM

Center of mass

Problem:

A uniform carpenter's square has the shape of an L, as shown in the figure.  Locate the center of mass relative to the origin of the coordinate system.

Solution:

• Concepts:
  The center of mass
• Reasoning:
  We are asked to find the CM of an object.
  We can think of the system as being made up of two subsystems, as shown in the figure.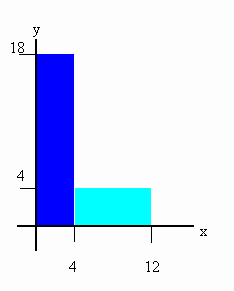

  

  The CM of the left subsystem lies at x_CM = 2 cm, y_CM = 9 cm.  The CM of the right subsystem lies at x_CM = 8 cm, y_CM = 2 cm.  If the mass of a 1 cm by 1 cm square is 1 unit, then the mass of the left subsystem is 72 units and the mass of the right subsystem is 32 units.  We find the CM of the system by treating each subsystem as a separate particle, with all its mass concentrated at its center of mass. 

• Details of the calculation:
  x_CM = (72 units 2 cm + 32 units 8 cm)/(104 units) = 3.85 cm,
  y_CM = (72 units 9 cm + 32 units 2 cm)/(104units) = 6.85 cm.
  The CM of the system lies outside of the system.  For irregular-shaped objects it is quite common for the CM to lie outside the system.  This special point outside the system responds to external forces as if the total mass of the system were concentrated there.

Moment of inertia

Problem:

The four particles in the figure below are connected by rigid rods.

The origin is at the center of the rectangle.  If the system rotates in the x-y plane about the z-axis with an angular speed of 6 rad/s, calculate
(a) the moment of inertia of the system about the z-axis and
(b) the rotational energy of the system.

Solution:

• Concepts:
  The moment of inertia about an axis, the rotational kinetic energy
• Reasoning:
  The moment of inertia is I = ∑m_ir_i².  Here r_i is the perpendicular distance of particle i from the z-axis.
  the rotational kinetic energy, T_rot = ½Iω²
• Details of the calculation:
  Each particle is a distance r = (9 + 4)^½ m = √(13) m from the axis of rotation.
  I = (3 kg + 2 kg + 4 kg + 2 kg)(13 m²) = 1 43 kgm².
  (b) The rotational kinetic energy is T_rot = ½Iω² = 71.5*36/s² = 2574 J.

Problem:

Three particles are connected by rigid rods of negligible mass lying along the y-axis as shown.

If the system rotates about the x-axis with angular speed of 2 rad/s, find
(a)  the moment of inertia about the x-axis and the total rotational kinetic energy evaluated from ½Iω², and
(b)  the linear speed of each particle and the total kinetic energy evaluated from ∑½m_iv_i².

Solution:

• Concepts:
  The moment of inertia of a system about an axis
• Reasoning:
  The moment of inertia is I = ∑m_ir_i². 
  Here r_i is the perpendicular distance of particle i from the x-axis.
• Details of the calculations:
  (a)  I = 4 kg 9 m² + 2 kg 4 m² + 3 kg 16 m² = 92 kgm².
  The rotational kinetic energy is T_rot = ½Iω² = 46*4/s² = 184 J.
  (b)  The linear speed of particle i is v_i = ωr_i.
  The linear speed of the 4 kg mass is v = 6 m/s, and its kinetic energy is ½mv² = 72 J.
  The linear speed of the 2 kg mass is v = 4 m/s, and its kinetic energy is ½mv² = 16 J.
  The linear speed of the 3 kg mass is v = 8 m/s, and its kinetic energy is ½mv² = 96 J.
  The sum of the kinetic energies of the three particles is 184 J.

Problem:

Two circular metal disks have the same mass M and the same thickness d.  Disk 1 has a uniform density ρ₁ which is less than ρ₂, the uniform density of disk 2.  Which disk, if either, has the larger moment of inertia about its symmetry axis perpendicular to the plane of the disk?

Solution:

• Concepts:
  The moment of inertia
• Reasoning:
  Let the radii of the disks be R₁ and R₂ respectively.
  The disks have the same mass and thickness.  Therefore ρ₁R₁² = ρ₂R₂².
  The moments of inertia are I₁ = MR₁²/2 and I₂ = MR₂²/2.
• Details of the calculation:
  I₁/I₂ = R₁²/R₂² =  ρ₂/ρ₁.
  Since ρ₁ < ρ₂, I₁ > I₂.  Disk 1 has the larger moment of inertia.

Problem:

Consider a rigid body consisting of a collection of point masses m_k at positions r_k in a body-fixed coordinate system. The system rotates with angular velocity Ω about an axis which passes through the origin of the space-fixed coordinate system.  The angular momentum of the system about the origin is L = Σ_kr_k×p_k =  Σ_km_kr_k×v_k = Σ_km_kr_k×(Ω × r_k).

(a)  Define the Cartesian components I_ij (i, j = x, y, z) of the inertia tensor, so that L_i = Σ_jI_ijΩ_j,  where the Ω_j are the components of Ω along the body-fixed axes.
(b)  Now assume a continuous mass distribution of uniform mass density ρ in a volume V having angular velocity Ω about an axis which passes through the origin.
Define the Cartesian components I_ij of of the inertia tensor for this mass distribution.

Solution:

• Concepts:
  The moment of inertia tensor.
• Reasoning:
  We are asked to define the moment of inertia tensor for a discrete and a continuous mass distribution.
• Details of the calculation:
  (a)  L = Σ_km_kr_k×(Ω × r_k) = Σ_km_k[r_k²Ω - r_k(r_k·Ω)].
  [A×(B × C) = (A·C)B - (A·B)C]
  We write this expression in component form.
  L_i = Σ_km_k[r_k²Ω_i - (x_k)_i(r_k·Ω)] = Σ_km_k[Σ_l(x_k)_l²Ω_i - (x_k)_iΣ_j(x_k)_j]Ω_j], or
  L_i = Σ_jΣ_km_k[Σ_l(x_k)_l²δ_ij - (x_k)_i(x_k)_j]Ω_j = Σ_jI_ijΩ_j
  I_ij = Σ_km_k[Σ_l(x_k)_l²δ_ij - (x_k)_i(x_k)_j].
  I_xx = Σ_km_k(y_k² + z_k²),  I_yy = Σ_km_k(x_k² + z_k²),  I_zz = Σ_km_k(x_k² + y_k²),
  I_xy = I_yx = -Σ_km_kx_ky_k,  I_xz = I_zx = -Σ_km_kx_kz_k,  I_yz = I_zy = -Σ_km_ky_kz_k.
  
  (b)  For a continuous mass distribution of uniform mass density ρ
  L = ρ∫dV [r²Ω - r(r·Ω)], and
  I_xx = ρ∫dV (y² + z²),  I_yy = ρ∫dV(x² + z²),  I_zz = ρ∫dV(x² + y²),
  I_xy = I_yx = -ρ∫dVxy,  I_xz = I_zx = -ρ∫dVxz,  I_yz = I_zy = -ρ∫dVyz.

Problem:

A cylinder with radius r, height h, and mass M has uniform mass distribution. 
(a)  Find the Cartesian components I_ij of its moment of inertia tensor in the body-fixed coordinate system shown in the figure.
(b)  If the cylinder is displaced along the z-axis so that its center of mass is at the origin, find the components I_ij in this new coordinate system.

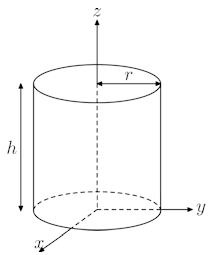
Solution:

• Concepts:
  The moment of inertia tensor.
• Reasoning:
  For a continuous mass distribution of uniform mass density ρ
  I_xx = ρ∫dV (y² + z²),  I_yy = ρ∫dV(x² + z²),  I_zz = ρ∫dV(x² + y²),
  I_xy = I_yx = -ρ∫dVxy,  I_xz = I_zx = -ρ∫dVxz,  I_yz = I_zy = -ρ∫dVyz.
• Details of the calculation:
  (a)  Here ρ = M/(πr²h) = constant.
  From symmetry I_xy = I_yx =  I_xz = I_zx = I_yz = I_zy = 0.  The coordinate axes are principal axes.
  I₃ = I_zz = ρ∫₀^hdz∫₀^rdr' 2πr'³ = 2πρhr⁴/4 = Mr²/2.
  From symmetry I_xx = I_yy or I₁ = I₂.
  2I₁ =  ρ∫dV (x² + y² + 2z²) =  Mr²/2 + 2ρ∫dV z².
  I₁ = Mr²/4 + [M/(πr²h)]πr²∫₀^hdz z² =  Mr²/4 + Mh²/3.
  (b)  The off-diagonal elements of the inertia tensor are still zero from symmetry.
  Parallel axis theorem:  I'_ii = I_ii + M(a² - a_i²) = I_ii + Ma_⊥² where I_ii refers to a body-fixed coordinate system with the origin at the CM and I'_ij refers to a coordinate system with parallel axes and a different origin.
  I_zz = I'_zz = Mr²/2.  I_xx = I_yy = I'_xx - Mh²/4 = Mr²/4 + Mh²/12.

Problem:

Find the fraction of the kinetic energy that is translational and rotational when
(a)  a hoop
(b)  a disc and
(c)  a sphere rolls down an inclined plane of height h.  Find the velocity at the bottom in each case.  Compare with a block sliding without friction down the plane.

Problem:

A uniform rectangular object of mass m with sides a and b (b > a) and negligible thickness rotates with constant angular velocity ω about a diagonal through the center.  Ignore gravity.

(a)  What are the principal axes and principal moments of inertia?
(b)  What is the angular momentum vector in the body coordinate system?
(c)  What external torque must be applied to keep the object rotating with constant angular velocity about the diagonal?