Consider a collection of water molecules.  Each proton in each molecule is a spin ½ particle with a magnetic moment m = γS, γ = g_nq_e/m_p (SI units).
If we place a sample in a uniform magnetic field B = (0,0,B₀), then, neglecting the interaction between different particles, the Hamiltonian of each proton is H = -m∙B = -m_zB₀.  (Here we treat the space coordinates macroscopically.)
H = -γB₀S_z = -ω₀S_z.
The eigenstates of H are the common eigenstates of S² and S_z, {|+>, |->}.  The eigenvalues are E ₊ = -ω₀ħ/2,  E_- = +ω₀ħ/2.

Assume a collection of water molecules, placed in uniform magnetic field B = (0,0,B₀), is in thermal equilibrium with its surroundings.  We then are dealing with a statistical mixture of states.  The density operator for the system is ρ = p₊|+><+| + p_-|-><-|.
p_± = N exp(-E_±/(kT)) = (1/Z) exp(-E_±/(kT)).
We have Tr(ρ) = <+|ρ|+> + <-|ρ|-> = (1/Z)(exp(ω₀ħ/(2kT)) + exp(-ω₀ħ/(2kT)) = 1.
The partition function Z is therefore given by Z = 2 cosh(ω₀ħ/(2kT)).
The density matrix at t = 0 in the {|+>, |->} basis is given by
.
How does the density matrix evolve?
(d/dt)ρ(t) = (1/(iħ))[H,ρ(t)]
The matrix of H in the {|+>, |->} basis is

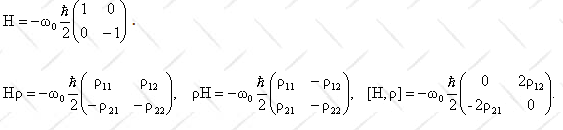
We therefore have
dρ₁₁/dt = 0,  dρ₂₂/dt = 0,  dρ₁₂/dt = iω₀ρ₁₂,  dρ₂₁/dt = -iω₀ρ₂₁.
This yields 

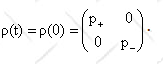
We can now calculate <S_x>, <S_y>, and <S_z> for our sample.
<S_x> = Tr(ρS_x).

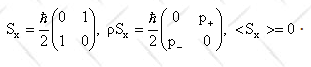
Similarly, <S_y> = 0.
<S_z> = Tr(ρS_xz). 
.
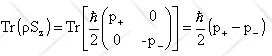The macroscopic magnetization M of the water sample is given by M = nγ<S>, where n is the number of protons per unit volume.  We therefore have M = (0,0,M_z) where M_z = nγ<S_z>.

Assume that at t = 0 a time-varying field B₁(t) is added to B₀.  Assume that for t > 0 we have B = (B₁cosωt, -B₁sinωt, B₀).  The z-component of B is constant, while the component of B perpendicular to the z-axis rotates cw about the z-axis with frequency ω.
Assume that B₁ << B₀.  The proton Hamiltonian is now given by
H(t) = -γS∙B(t) = -γB₀S_z - γB₁(cosωt S_x - sinωt S_y) = -ω₀S_z - ω₁(cosωt S_x - sinωt S_y),
with ω₁ = γB₁.

Consider the state vector |ψ(t)> describing a single proton, |ψ(t)> = U(t,0)|ψ(0)>.
Let R(φ) describe a ccw rotation about the z-axis and let U(R) be the rotation operator for the ccw rotation R(φ).
U(R) = exp(-(i/ħ)S_zφ).
We have
|ψ(t)> = U(t,0)|ψ(0)>,  U(R)|ψ(t)> = U(R)U(t,0)|ψ(0)>.
U(R) can be viewed as an operator that rotates every state vector ccw through an angle φ or an operator that changes the basis vectors and therefore rotates the coordinate system cw through an angle φ.
Let φ = ωt, then U(R) rotates the coordinate system cw with angular frequency ω.  The coordinate system thus rotates with the magnetic field cw about the z-axis.

Consider an infinitesimal rotation and an infinitesimal time interval dt.
U(R)|ψ(dt)> = (I - (i/ħ)S_zωdt)|ψ(dt))> = (I - (i/ħ)S_zωdt)(I - (i/ħ)Hdt)|ψ(0)>.
U(R)|ψ(dt)> = (I - (i/ħ)S_zωdt)(I - (i/ħ)(-ω₀S_z - ω₁(cosωt S_x - sinωt S_y))dt)|ψ(0)>.
U(R)|ψ(dt)> = (I - (i/ħ)((ω - ω₀)S_z - ω₁S_xcosωt + ω₁S_ysinωt)dt)|ψ(0)>.

S is a vector observable, its components transform under a rotation R as V’ = R^-1V.
For a cw rotation R^-1(φ) we have V_x’ = V_xcosφ - V_ysinφ.
Therefore S_x’ = S_xcosωt - S_ysinωt is the x-component of the observable S in a frame that rotates cw with angular frequency ω about the z-axis, i.e. in a frame that rotates with the magnetic field. 
We therefore have  U(R)|ψ(dt)> = |ψ'(dt)> = (I - (i/ħ)((ω - ω₀)S_z - ω₁S_x’)dt)|ψ(0)>.
|ψ'(dt)> = (I  -(i/ħ)((ω - ω₀)S_z’ - ω₁S_x’)dt)|ψ’(0)>
|ψ'> denotes the state vector in a frame rotating cw about the z-axis with angular frequency ω.
In this frame the evolution operator is U(t,0) = exp(-(i/ħ)((ω - ω₀)S_z’ - ω₁S_x’)t).
Let ω = ω₀. 
Then |ψ'(dt)> = (I + (i/ħ)ω₁S_x’dt)|ψ’(0)>.  The infinitesimal evolution operator is I + (i/ħ)ω₁S_x’dt and the evolution operator is U(t,0) = exp((i/ħ)ω₁S_x’t).
The Hamiltonian therefore is H’ = -ω₁S_x’.
The matrix of the Hamiltonian is

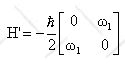
in the {|+>, |->} basis.

At t = 0 the lab frame and the frame that rotates with B coincide.  The density matrix at t = 0 in the {|+>, |->} basis is given by
.
Since H’ = -ω₁S_x’ it is convenient to change the basis.  In the {|+>_x, |->_x} eigenbasis of S_x the density matrix is given by U^†ρ(0)U, where U is the unitary transformation that transforms {|+>, |->} into {|+>_x, |->_x}.
The matrix of U is  
. 
In the {|+>_x, |->_x} basis we have
.
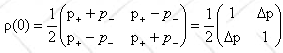Here Δp = p₊ - p_-.
The matrix of S_x in the {|+>_x, |->_x} basis is
. 
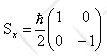Let us now calculate ρ(t) in the reference frame rotating with B. 
(d/dt)ρ'(t) = (1/(iħ))[H',ρ'(t)].
The matrix of H' in the {|+>_x, |->_x} basis is

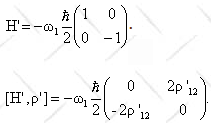
We therefore have

dρ₁₁/dt = 0,  dρ₂₂/dt = 0,  dρ₁₂/dt = iω₁ρ₁₂,  dρ₂₁/dt = -iω₁ρ₂₁.
This yields  ρ₁₁(t) = 1/2,  ρ₂₂(t) = 1/2,  ρ₁₂(t) = -exp(iω₁t) Δp/2,  ρ₂₁(t) = exp(-iω₁t) Δp/2.
We can now calculate <S’_x>, <S’_y>, and <S’_z> in the rotating frame.
<S’_x(t) > =Tr(ρ'(t)S’_x).
.
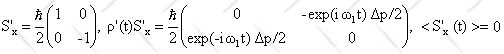In the {|+>_x, |->_x} basis the matrix of S_y is 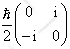and the matrix of S_z is  .
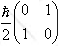In the rotating reference frame we therefore have

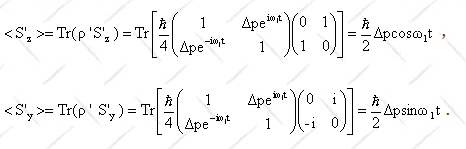
In the rotating frame the magnetization rotates clockwise about the x’-axis.  There are times when the magnetization has only a z-component, and times when it entirely lies in the plane perpendicular to the z-direction.

What do we observe in the lab frame?
S is a vector observable.  The expectation values of the components of a  of a vector observable behave under rotation as though the observable were a classical vector.  We have
<S_i'> = ∑_iR_ij<S_j>,  <S_i> = ∑_iR_ij^-1<S_j'>.
R(φ) is a ccw rotation about the z-axis.
The matrix of R^-1 is  

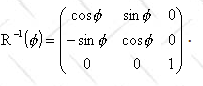
We therefore have (with ω = ω₀)
<S_x> = <S’_x>cosω₀t + <S_y’>sinω₀t = (ħ/2)Δp sinω₁t sinω₀t,
<S_y> = -<S’_x>sinω₀t + <S_y’>cosω₀t = (ħ/2)Δp sinω₁t cosω₀t,
<S_z> = <S’_z> = (ħ/2)Δp cosω₁t.
The macroscopic magnetization M = nγ<S> of the water sample changes from nγ(ħ/2)Δp to -nγ(ħ/2)Δp and back.  Since B₁ << B₀ and the eigenstate of the unperturbed Hamiltonian are not degenerate, the eigenstates of the perturbed Hamiltonian are approximately equal to |+> and |->, and the eigenvalues are approximately -(ħω₀/2) and +(ħω₀/2).  When the magnetization changes from nγ(ħ/2)Δp to -nγ(ħ/2)Δp, many protons make transitions from the |+> to the |-> state.  They have to absorb energy from the field.  When the magnetization changes back to nγ(ħ/2)Δp, energy is dumped back into the field.

NMR
A continuous wave experiment can be performed by sweeping the frequency of the rotating field B₁ through the resonance frequency ω₀ and by monitoring the power output of the power supply that supplies the current that produces B₁.  Oscillations in the power output indicate that the frequency is sweeping through the resonance frequency.  If γ is known, ω₀ = γB₀ yields B₀.  In this way the strength of an unknown magnetic field can be measured.  If B₀ is known, ω₀ = γB₀ yields γ.  Instead of sweeping the frequency ω of the rotating field, a continuous wave experiment can also be performed by sweeping B₀ while holding ω constant.

Experiments can also be performed with pulsed magnetic fields.  Assume that at time t₁ = π/(2ω₁) we turn off B₁.  Then for t > t₁ H = -ω₀S_z.  In the lab frame we have
<S_x> = (ħ/2)Δp sinω₀t₁, <S_y> = (ħ/2)Δp cosω₀t₁, <S_z> = 0  at t = t₁.  

At t = t₁ the magnetization lies in the x-y plane.  How does it evolve?
To find the density matrix ρ(t₁) in the lab frame in the {|+>, |->} basis we can use
<S_x> = Tr(ρ,S_x), or (ħ/2)Δp sinω₀t₁  = (ħ/2)(ρ₁₂ + ρ₂₁) = ħ Re(ρ₁₂),  Re(ρ₁₂) = ½Δpsinω₀t₁,
<S_y> = Tr(ρ,S_y), or (ħ/2)Δp cosω₀t₁ = i(ħ/2)(ρ₁₂ - ρ₂₁) = -ħ Im(ρ₁₂),  Im(ρ₁₂) = -½Δpcosω₀t₁,
<S_z> = Tr(ρ,S_z), or 0 = (ħ/2)(ρ₁₁ - ρ₂₂),  ρ₁₁ = ρ₂₂ = ½, since the trace is 1.
 .

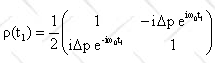For t > t₁ we have dρ₁₁/dt = 0,  dρ₂₂/dt = 0,  dρ₁₂/dt = iω₀ρ₁₂,  dρ₂₁/dt = -iω₀ρ₂₁,
which yields


For t > t₁ we therefore have
<S_x(t)> = Tr(ρ(t),S_x) = (ħ/2)Δp sinωt,
<S_y(t)> = Tr(ρ(t)S_y) = (ħ/2)Δp cosωt,
<S_z(t)> = 0.
The magnetization lies in the x-y plane and rotates cw about the z-axis.  As the magnetization rotate about the z-axis, it will induce a current in a pick-up coil located with its axis along the x-axis.  Plotting this current versus time yields a sinusoidal wave form.  This current will decay as a function of time due to dephasing.  This is called free-induction decay.  The spin-spin relaxation time T₂ is the time with which the transverse magnetization decays.  M_xy = M_xy0e^-t/T2.  Loss of transverse magnetization is due to molecular interactions and field inhomogeneity.

At equilibrium the net magnetization is M = (0,0,M_z).  As we have seen, it is possible to make M_z = 0.  The time constant with which M_z returns back to its equilibrium value is called the spin-lattice relaxation constant T₁.  M_z = M₀(1 - e-^t/T1).  Spin lattice relaxation is the result of the nuclei transferring energy to the surrounding molecules as thermal energy.

In pure water T₁ ~ T₂ ~ 2s - 3s.  In biological materials T₂ < T₁.

Reference:

The Basics of MRI
Note the chapters on spin physics and NMR spectroscopy