Summary: Adding two angular momenta

Vectors in the subspace E(j₁,j₂) may be expanded in terms of or basis vectors.  The basis vectors of one basis can be written as linear combinations of basis vectors of the other basis.

.

The expansion coefficients are called the Clebsch-Gordan coefficients.  Sometimes the Clebsch-Gordan coefficients are written in terms of the Wigner 3-j symbols.  We have

Properties of the Wigner 3-j symbols:

We can permute the columns of the 3-j symbol.  An even permutation does not alter its value.  An odd permutation multiplies the initial value by .  Moreover,

.

This implies

or

Adding more than two angular momenta

When adding the angular momenta j₁, j₂, and j₃, many different states of the system may correspond to the same value of j and m.

Let

Then

The Racah W coefficients and 6-j symbols transform from one scheme of adding three angular momenta to another.

The 9-j symbols transform from one scheme of adding four angular momenta to another.

Links:

• Racah coefficients, 6-j symbols, 9-j symbols
• 3-j, 6-j, and 9-j symbol calculators (1)
• 3-j, 6-j, and 9-j symbol calculators (2)

We will now establish a connection between the Clebsch-Gordan coefficients and the matrix elements of operators that transform like the spherical harmonics under rotation.

The rotation matrices

Angular momentum and rotations are closely linked.  Let us, for a moment, return to the rotation matrices.  An arbitrary rotation can be accomplished in three steps, known as Euler rotations, and it is therefore characterized by three angles, known as Euler angles.  We may proceed as follows.

First rotate the body ccw about the z-axis by an angle a.  Then rotate ccw about the y’-axis by an angle b.  Finally rotate ccw about the z’-axis by an angle g.

The rotation matrix is R(a,b,g)=R_z’(g)R_y’(b)R_z(a).  (Note: In quantum mechanics it is advantageous to perform the second rotation about the y’-axis.  In classical mechanics the second rotation is often performed about the x’-axis.)  R_z’(g) and R_y’(b) are rotations about body-fixed axis.  We want to express these rotations in terms of rotations about space-fixed axis.  We may write R_y’(b)=R_z(a)R_y(b)R_z^-1(a). Similarly, R_z’(g)=R_y’(b)R_z(g)R_y’^-1(b). We can now rewrite R(a,b,g) as

R(a,b,g)=R_z’(g)R_y’(b)R_z(a). 
=R_y’(b)R_z(g)R_y’^-1(b)R_y’(b)R_z(a)
=R_y’(b)R_z(g)R_z(a)
=R_z(a)R_y(b)R_z^-1(a)R_z(g)R_z(a)
=R_z(a)R_y(b)R_z(g).  Rotations about the same axis commute.)

The rotation operator U(R(a,b,g)) therefore may be written as

U(R(a,b,g))=U(R_z(a))U(R_y(b))U(R_z(g)).

It only involves rotations about space-fixed axis.  We already know the rotation operators for rotations about space-fixed axes. (See notes.)

For a spin ½ particle U(R(a,b,g))=U(R_z(a))U(R_y(b))U(R_z(g)) becomes

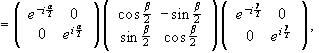
using

.

(See notes.)

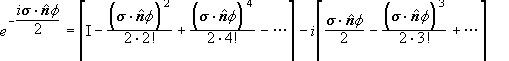
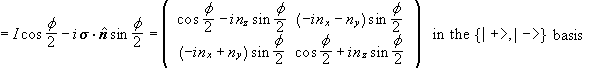The matrix elements of the second rotation are purely real.  This is a result of choosing the y’-axis for our second Euler rotation.

For a system with angular momentum J the matrix elements of the rotation operator in the subspace E(j) in the {|j,m>} basis for a rotation R(n,q) are 

U^j _m',m(R)=<j,m'|exp(-iJ×nq/h)|j,m>. 

In E matrix elements between states with different values j vanish.  In E the matrix of the rotation operator is block diagonal.  U^j(R) is referred to as the (2j+1)-dimensional irreducible representation of the rotation operator U(R).  The U^j(R) form a group.

The matrix elements of the rotation operator, for the rotation R(a,b,g) are

The only part which mixes different m values is the middle rotation.  We can define a new matrix d^j with elements

 ,

which contains the nontrivial part of the rotation matrix U^j(a,b,g) .  The matrix elements are also listed on the standard table of Clebsch-Gordan coefficients.

We can establish a connection between the rotation operator and the spherical harmonics by constructing the state vector ( This state vector is an eigenvector of the position operator.)

Let and  Then

and

(Matrix elements between states with different values l vanish.)

We have

We therefore have

or

This is the connection between the rotation operator and the spherical harmonics.  When m = 0 then

Transformation properties of the spherical harmonics

How do the spherical harmonics transform under rotation?

Let

Then

But , therefore

The function can also be viewed as an operator in coordinate space.  (It could, for example, be the operator of an experiment that measures an emission pattern and projects it onto a known distribution.)  The coordinate representation of this operator operating on the state vector |y> is y(r), just as the coordinate representation of the operator X operating on the state vector |y> is xy(r).

Rotating the observable we obtain

. (See notes.)

[U(R)|r>=|Rr>,  U(R)y(r)=y(R^-1r),  U^T(R)y(r)=y(Rr),

U^T(R)Y_lm(n)y(r)=Y_lm(Rn)y(Rr), 

U^T(R)Y_lm(n)U(R)y(r)=U^T(R)Y_lm(n)y(R^-1r)=Y_lm(Rn)y(r)=Y_lm(n')y(r)]

We may therefore write

We define as an irreducible tensor operator of rank k any set of 2k+1 quantities that transform like the spherical harmonics Y_kq under rotation.

T^k_q is an irreducible or spherical tensor of rank k with 2k+1 components if

or, equivalently

or

Considering the infinitesimal form of this expression we have

or, multiplying out the terms,

This yields

.

The two commutation relations can also be taken as a definition of a spherical tensor of rank k.

Examples of tensor operators:

• A scalar operator is an irreducible tensor of rank 0.  It consist of one component and commutes with all components of the angular momentum J.  It therefore fulfills the commutation relations that define a spherical tensor of rank 0.
• The spherical components of a vector operator A are defined as

  

  Using our definition of a vector operator we can show that these components satisfy the commutation relations that define a spherical tensor of rank 1.  For example,

   etc.

  A vector operator therefore is a spherical tensor operator of rank 1.

• A Cartesian tensor is defined through
  Let A and B be two vectors, then T_ij=A_iB_j are the elements of a Cartesian tensor.  Cartesian tensors are reducible, they can be decomposed into objects that transform differently under rotation. For T_ij=A_iB_j we have

  

  is a scalar, represents three independent components which transform like a vector.

    represents the components of a traceless, symmetric tensor with 5 independent components.  T_ij has been decomposed into three objects that transform like the spherical harmonics with l = 0, 1, and 2 respectively. It has been decomposed into irreducible spherical tensors.

The Wigner-Eckart theorem

Why do we care about tensor operators?

The matrix elements of tensor operators with respect to angular momentum eigenstates satisfy

The double bar matrix element is independent of m, m’, and q.  This is the Wigner-Eckart theorem.
(In the above equation (2j'+1)^-1/2 is factored out of the double bar matrix element.  This factoring is not unique. Different books may factor out a different factor.)

The matrix element  is written as the product of two factors.  The first factor is a Clebsch-Gordan coefficient which depends only on the way the system is oriented with respect to the z-axis.  It does not depend on the physical nature of the particular tensor operator.  The second term depends on the physical nature of the operator and the system, but it does not depend on the magnetic quantum numbers m, m’, and q. To evaluate for the various combinations of m, m’, and q we need to only evaluate one matrix element.  The others are related via the Clebsch-Gordan coefficients.

Certain selection rules for tensor operators follow directly from the selection rule of the Clebsch-Gordan coefficients.  The matrix element is zero unless m’=m+q and

Using the commutation relations that define a tensor operator we have

• 

  

• 

  yields

  

  

  or

  

  

  

• Similarly we evaluate the matrix elements of

We find the same recursion relations for the as we found for the Clebsch-Gordan coefficients with j₁=j, j₂=k, and j=j’, m₁=m, m₂=q, and m=m’ .  Therefore the m behavior of the must be the same as that of the Clebsch-Gordan coefficients.  We write